Ganz allgemein ist ja leider festzustellen, daß alle bisherigen in der chemischen Technik und Verfahrenstechnik angewendeten Zustandsgleichungen, selbst die modernsten, nicht in der Lage sind, die realen pvT- Verhältnisse eines Stoffes mit ausreichender Genauigkeit in der kritischen Region darzustellen. Das bestätigen Aussagen zur Genauigkeit in der kritischen Region z. B. auch in der wichtigen und modernen web- site „nist webbook“, die pvT- Werte oft angewendeter Stoffe der chemischen Industrie mit den aktuell besten empirischen Zustandsgleichungen nach Anpassung an Meßwerte angibt (s. auch den Artikel „Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region“ vom 15.4.2013). Auch die Erwartung, daß sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne oder geringe empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Mit nun vorliegenden Untersuchungsergebnissen zum pvT- Verhalten reiner Stoffe in der kritischen Region ist versuchsweise ein Theorie- Ansatz abgeleitet worden, der zu einer Erweiterung von Gesetzmäßigkeiten kritischer Phänomene weit über ihre bisherige Anwendbarkeit begrenzt auf die nahe Umgebung des kritischen Punktes führt. So ergeben sich z. B. Berechnungsgleichungen für die kritische Isotherme und benachbarte Isothermen, die die pvT- Verhältnisse in der Nähe des kritischen Punktes eines Stoffes allein nur bei Kenntnis der kritischen Daten pk, vk, Tk bei guter Annäherung an die Realität wiedergeben. Allerdings ist dieser Ansatz außerhalb des bisherigen Main- Streams. Die von manchen theoretischen Physikern vertretene Ansicht, kritische Exponenten seien analog einer Naturkonstanten unabhängig vom Stoff und etwa konstant, bestätigt sich mit diesem Theorie- Ansatz nur teilweise. Der kritische Exponent β bestätigt sich stoffunabhängig mit ca. 1/3, der Exponent δ allerdings erweist sich als stoffabhängig berechenbar mit den kritischen Daten.
Die van der Waals- Thermodynamik und die vielen auf dieser Grundlage abgeleiteten Zustandsgleichungen gelten ja nicht in der kritischen Region. Hier gelten die Gesetzmäßigkeiten kritischer Phänomene, deren Wirksamkeit nachgewiesen und von der Theorie her erklärt ist- aber doch noch nicht soweit entwickelt ist, dass man für technische Zwecke verlässlich damit rechnen könnte. Veröffentlichte Stoffwerte für Zustände in der kritischen Region können deshalb mit erheblichen Fehlern behaftet sein, wie die Autoren von Stoffwertdaten selbst einschätzen. Die Situation der Bestimmung von Zustandsdaten in der Umgebung des kritischen Punktes eines Stoffes ist bereits in verschiedenen Artikeln dieses Blogs näher dargestellt: „Die Anwendbarkeit kritischer Phänomene zur Berechnung von pvT- Daten“ vom 23.2.2013; „Zur Genauigkeit der Berechnung von pvT-Daten in der kritischen Region“ vom 15.4.2013. Die in Datensammlungen und in der Literatur beschriebenen Berechnungsgrundlagen beziehen sich auf supergenaue Messungen in der kritischen Region und auf jeweils weitgehende empirische Zustandsgleichungen für technisch wichtige Stoffe. Allgemeingültige Lösungen ausreichender Genauigkeit können nicht genannt werden.
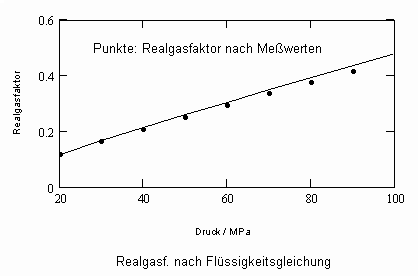
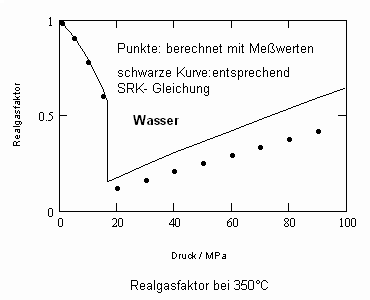
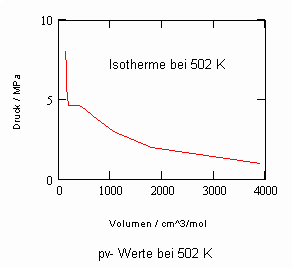
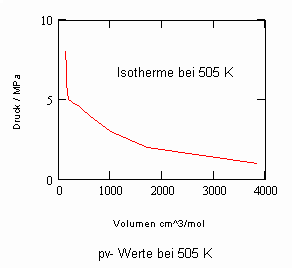
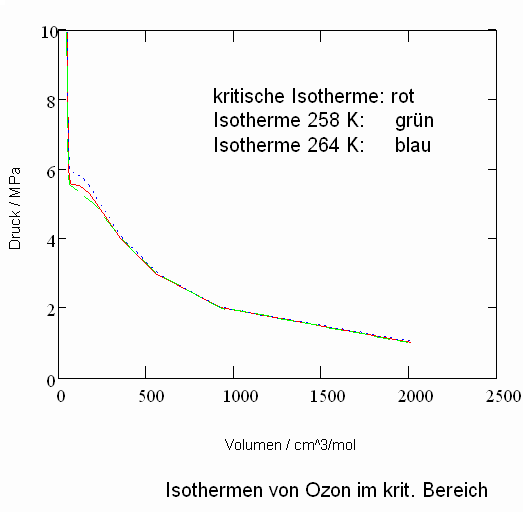
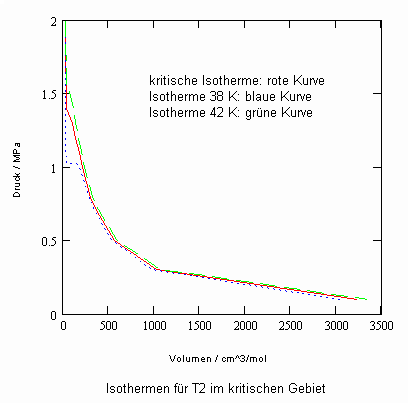
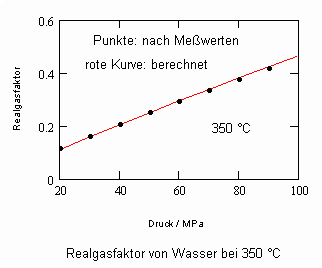
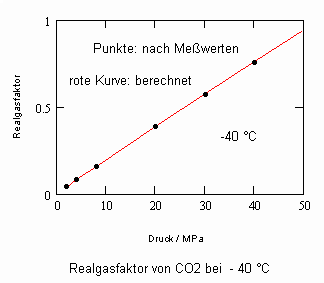
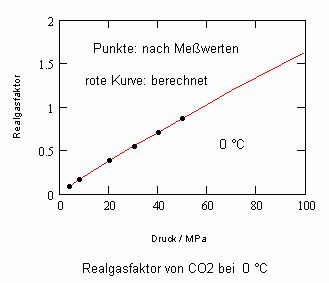
Nun ergab es sich nach den o. gen. speziellen Untersuchungen des Verhaltens von Stoffen in der kritischen Region, dass eine Hypothese zur näherungsweisen Erweiterung des Gültigkeitsbereichs kritischer Phänomene sowohl für Zustände um den kritischen Punkt als auch für Zustände weiter entfernt vom kritischen Punkt zu der Realität weitgehend nahekommenden Ergebnissen führt (Angaben zur Theorie und ihre Anwendungen s. z. B. den Artikel „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ vom 1.5. 2009). Nachrechnungen der pv- Daten kritischer Isothermen gut vermessener Stoffe zeigen das, indem die Berechnungsergebnisse entsprechend der neuen zur Theorie kritischer Phänomene abgeleiteten Möglichkeiten mit Ergebnissen von bisher angewendeten Zustandsgleichungen- dokumentiert in „nist webbook“- verglichen werden. Zu betonen ist, dass zur Bestimmung der pv-Werte auf der kritischen Isotherme entsprechend der neuen Berechnungsmöglichkeiten nur die Kenntnis der kritischen Daten pk, vk, Tk notwendig ist, während die von renommierten Autoren angewendeten weitgehend empirischen Zustandsgleichungen umfangreiche Messungen und Anpassungen erfordert haben. Beispiele zum Vergleich der Ergebnisse des neuen Theorie- Ansatzes mit denen nach herkömmlichen weitgehend empirischen Zustandsgleichungen renommierter Autoren auf der Grundlage sehr genauer Messungen und Anpassungen können nach Anforderung (dr.f.tampe@t-online.de) zur Verfügung gestellt werden (für Benzol, Toluol, Ethylen, Kohlenstoffdioxid, Propylen, Helium, Wasserstoff, Methanol…usw.). Auch verwendbare Nachrechnungen für pvT- Daten von Stoffen, zu denen keine Meßwerte außer denen der kritischen Daten in der kritischen Region existieren, sind nun vorstellbar! Das ist durchaus für bisher nicht weiter vermessene Stoffe bei nur der Kenntnis der kritischen Daten zu erwarten (entsprechende Anfragen ebenfalls an die o.gen. Mail- Adresse bei kostenloser Bearbeitung, falls die Ergebnisse nach Absprache zur Auswertung benutzt werden dürfen).
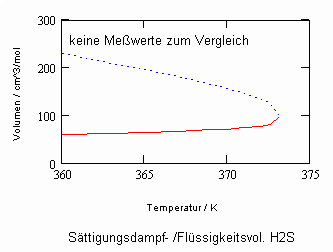
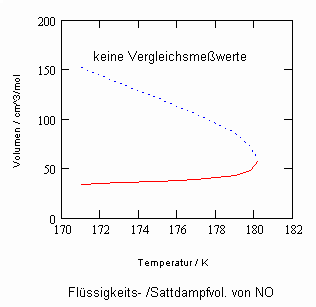
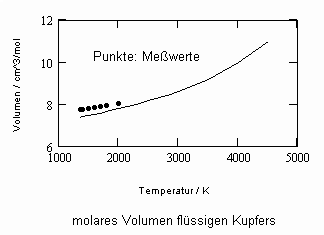
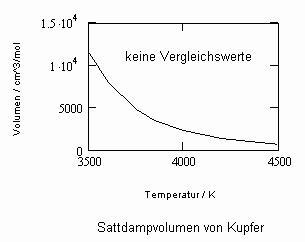
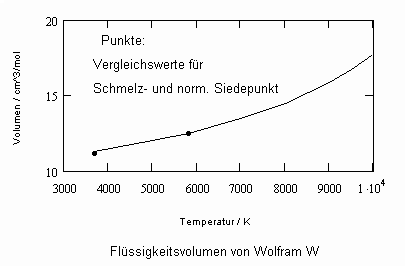
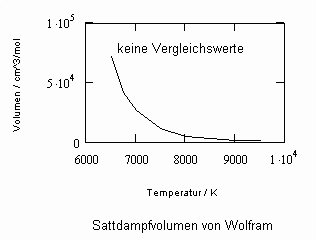
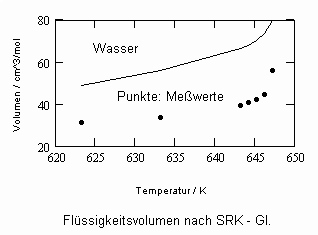
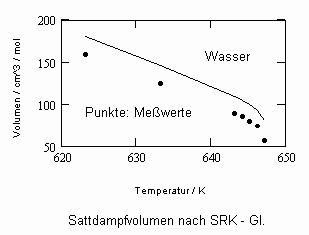
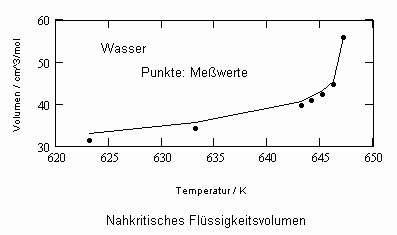
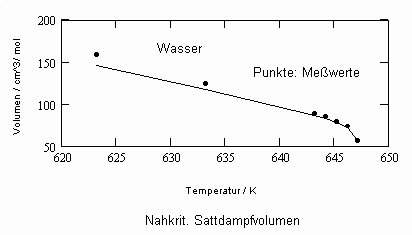
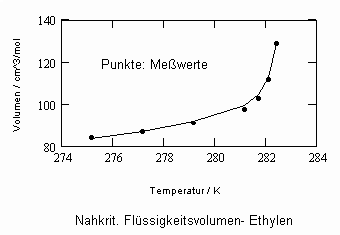
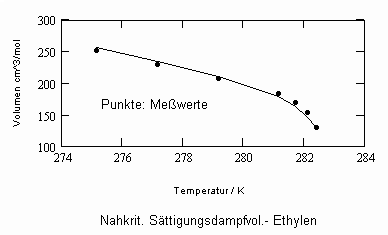
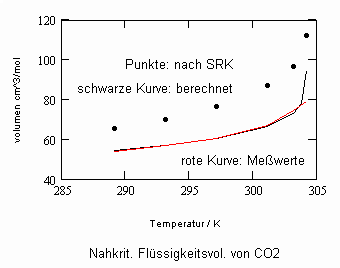
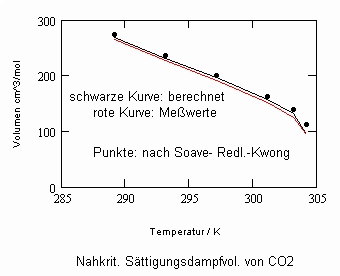
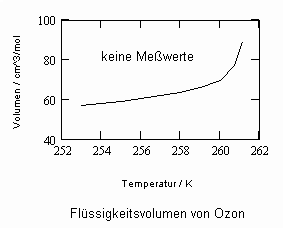
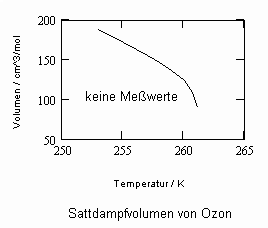
Sehr interessant ist es auch, dass es mit den neuen Möglichkeiten zur Berechnung von pv- Daten auf Isothermen möglich ist, die Sättigungsdaten v‘, v“ von Flüssigkeiten und Dämpfen entsprechend der Temperatur als Näherungen zu bestimmen. Für die v‘-, v“-Volumina von Stoffen kurz unter der kritischen Temperatur eines Stoffes und weiter entfernt von der kritischen Temperatur können so Berechnungsgleichungen abgeleitet werden. Diese Gleichungen geben die Sättigungsvolumina von Flüssigkeiten und Dämpfen als Temperaturfunktion und als Näherung an. Die Genauigkeit der Flüssigkeitsdaten ist dabei oft recht hoch und entsprechend von Meßwerten erheblich besser als die der Dampfdaten. Anfragen zu solchen Nachrechnungen o. gen. Art sind möglich. Es ist darauf hinzuweisen, daß es bisher keine allgemein gültige Möglichkeit gibt, die Sättigungsvolumina von Stoffen als Näherung zu berechnen.
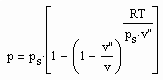
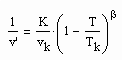
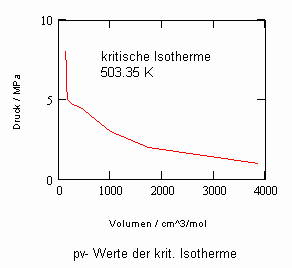
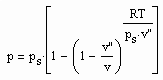 , (I)
, (I)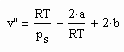 . (II)
. (II)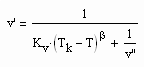 . (IV)
. (IV)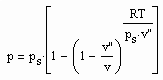 (1)
(1)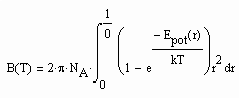 . (3)
. (3)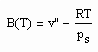 . (4)
. (4)
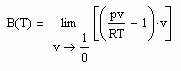 (5)
(5)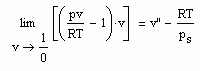
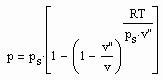 (1)
(1)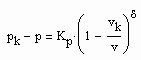 (2)
(2)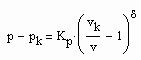 (3)
(3)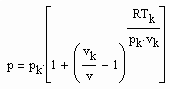 v‹ vk (4)
v‹ vk (4)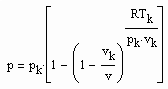 v›vk (5)
v›vk (5)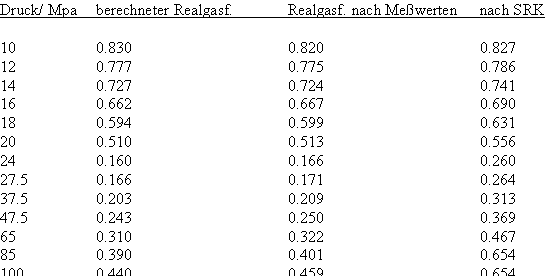

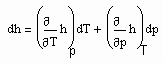 . (7)
. (7)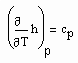 (8)
(8) (9)
(9)



 ,
,
 ,
, .
.