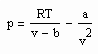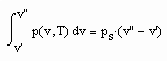In atomistischer Betrachtungsweise ist ein Festkörper bzw. ein Kristall mit einer starren Anordnung seiner Gitterbausteine aufgebaut. Die Gitterbau-steine können Schwingungen gegeneinander ausführen. Das Verhalten und das energetische Niveau des Festkörpers werden wesentlich von den Schwingungen der Gitterbausteine bestimmt. Die von den Gitterbausteinen des Festkörpers ausgeführten Schwingungen entsprechen den Wechselwirkungen im Gitter.
Fehlt die zwischenmolekulare Wechselwirkung vollständig, liegt ein ideales Gas vor. Beim Beginn zwischenmolekularer Wechselwirkungen der Moleküle bzw. der Atome des Stoffes liegt ein reales Gas vor.
Beim Festkörper bzw. Kristall tritt beim Übergang zur Flüssigkeit eine Fluktuation der Molekülpositionen auf.
Der Unterschied zwischen einer Flüssigkeit und einem realen Gas äußert sich im Verhältnis von kinetischer Energie und potientieller Energie der Moleküle bzw. Atome des Gases. Die kinetische Energie des Gases ist größer als die potientielle und es existiert eine freie Weglänge , die viel größer als die Ausdehnung der Molekülwechselwirkungen ist.
Flüssigkeiten entsprechen also Zuständen zwischen realen Gasen und Festkörpern.
Eine wichtige Grundlage zur Beschreibung des Verhaltens realer Gase ist bekanntlich die van der Waals- Gleichung. Sie ist der Ausgangspunkt für viele Weiterentwicklungen- aber dann immer auf weitgehend empirischer Basis.
Die klassische van der Waals- Gleichung beschreibt die Zustände realer Gase und sogar auch von Flüssigkeiten qualitativ richtig, quantitativ aber zur Auslegung technischer Abläufe keineswegs ausreichend. Die Ungenauigkeiten im Zweiphasengebiet und für Daten in der Nähe des kritischen Punktes können groß sein. Vor allem Flüssigkeitszustände werden sehr ungenau oder gar nicht erfaßt. Diese Feststellungen betreffen keineswegs nur die van der Waals- Gleichung, sondern auch die in der Technischen Thermodynamik entstandenen sogen. „halbempirischen Zustandsgleichungen“ von Soave, Redlich, Kwong und Peng, Robinson u. a. , die heute weltweit zur Berechnung von Zustandsdaten angewendet werden.
So ist es bis heute nicht gelungen, die physikalische Theorie so zu entwickeln, daß die Volumina bzw. Dichten von Stoffen temperaturabhängig entlang der Dampfdruckkurve mit genügender Genauigkeit von der Schmelztemperatur bis zur kritischen Temperatur berechnet werden können. Oftmals besteht auch die Situation, daß mit den gegebenen Gleichungen zwar das Dampf- und Gasverhalten gut erfaßt werden kann, nicht aber die Flüssigkeitswerte.
Die heutigen thermischen Zustandsgleichungen als Grundlage der Berechnung von Stoffdaten für Flüssigkeiten und Gase beruhen alle letztlich auf der physikalisch begründeten van der Waals- Gleichung, der Virialgleichung, auf Ansätzen der statistischen Thermodynamik und vor allem auf Parameter- Anpassungen der Berechnungsgleichungen an Meßwerte. Die empirische Vielfalt ist für einen Praktiker kaum noch überschaubar.
Die unter Physikern manchmal ironisch geäußerte Kritik, daß die sogen. „halbempirischen Zustandsgleichungen“ der Verfahrenstechnik und Technischen Thermodynamik ein selbst empirisch erforderliches Niveau ja eigentlich nur zur Hälfte erfüllen, charakterisiert die Situation.
Die Theoretische Physik muß trotz der unbezweifelbaren verfahrenstechnischen Empirie – Erfolge Richtschnur im Labyrinth der Möglichkeiten bleiben. Die Suche nach physikalisch begründeten neuen Ansätzen mit geringeren empirischen Anteilen sollte gerade auf dem Gebiet der Berechnung von p,v,T- Daten aktuell sein und bleiben.
Wenig untersucht ist die Möglichkeit, Gesetzmäßigkeiten der physikalischen Theorie kritischer Phänomene auszuwerten und sogar evtl. auf die Berechnung thermophysikalischer Daten anzuwenden.
Kritische Phänomene sind für nahkritische Zustände eines Stoffes erklärt als spezielle und weitgehend allgemeingültige Abhängigkeiten zwischen Druck, Temperatur, Volumen, Wärmekapazität usw. Wichtig ist evtl. der Schritt, den Versuch zu unternehmen, Gesetzmäßigkeiten kritischer Phänomene auch auf Zustände weiter ab vom kritischen Zustand als Näherung anzuwenden.
Beispielsweise erweist es sich alternativ auf solch einer Grundlage als durchaus möglich, die Siededichten von Stoffen mit hoher Genauigkeit zu berechnen, ohne auch nur eine der heute üblichen Zustandsgleichungen zu benutzen. Es muß dazu jeweils nur der kritische Druck, die kritische Temperatur und ein weiterer Datenpunkt mit Angaben für Temperatur, Druck und Dichte für einen Zustand niedrigen Dampfdrucks (z. B. beim normalen Siedepunkt) vorliegen (Parameter wie ω als azentrischer Faktor und alle anderen mit vielen empirischen Voraussetzungen erklärten Parameter sind gar nicht notwendig!).
Selbst Realgasfaktoren für reale Gase und sogar Flüssigkeiten unter hohem Druck können so als Näherung berechnet werden- ohne die Verwendung einer der bisher üblichen Zustandsgleichungen.
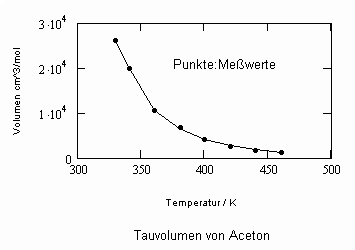
Auch Taudichten eines Stoffes lassen sich auf der Grundlage von Gleichungen, die sich aus Gesetzmäßigkeiten kritischer Phänomene ergeben, näherungsweise berechnen.
Der alternative Ansatz über die Theorie kritischer Phänomene in Verbindung mit herkömmlichen molekulartheoretischen Vorstellungen- wie sie z.B. zur Herleitung der van der Waals- Gleichung notwendig waren- führt zu neuen Berechnungsmöglichkeiten für Zustände realer Gase und für Flüssigkeiten. Der Zugang zu einer allgemeinen Theorie der Flüssigkeiten wird dadurch evtl. nicht auf der Grundlage bisheriger Ansätze und Vorstellungen auf rein molekulartheoretischer Grundlage und der statistischen Thermodynamik, sondern in Verbindung dieser Grundlagen mit der physikalischen Theorie kritischer Phänomene ermöglicht. Allerdings ist zu sagen, daß zu all diesen alternativen Möglichkeiten der Übertragung von Gesetzmäßigkeiten kritischer Phänomene auf die Berechnung von Zuständen weiter entfernt von den kritischen Daten die physikalische Begründung letzlich noch fehlt. Hier besteht Forschungsbedarf! Klar aber ist, daß sich mit den abgeleiteten neuen Gleichungen als Näherungen richtig rechnen läßt. Die Überprüfung dieser Möglichkeiten erfolgte durch die Nachrechnung an gut vermessenen Stoffbeispielen.
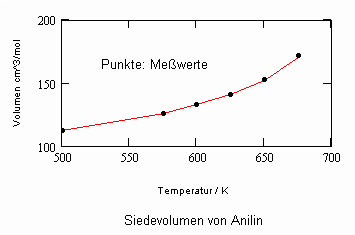
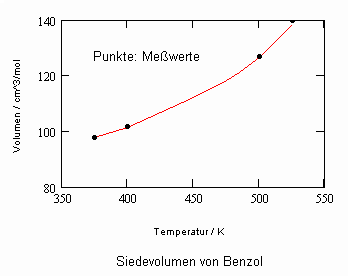
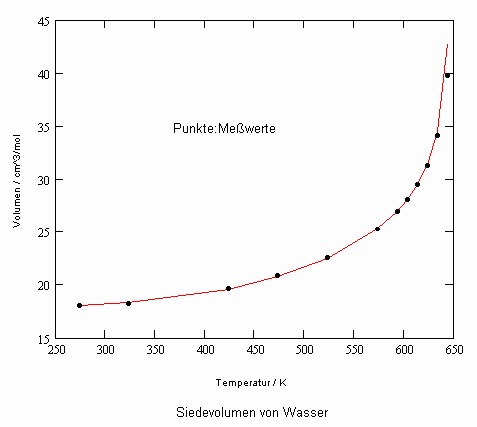
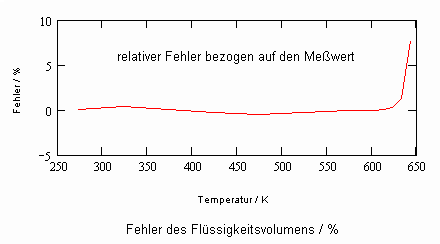
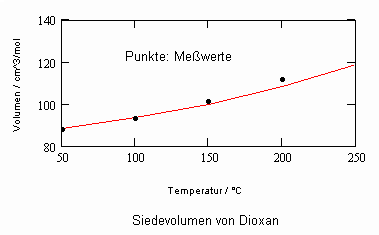
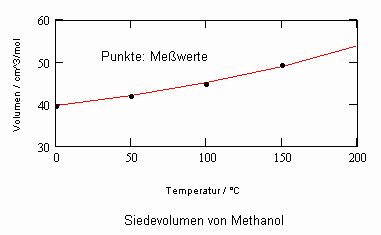
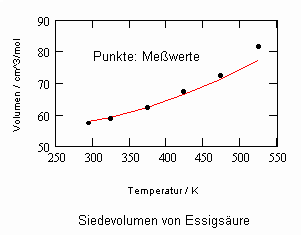
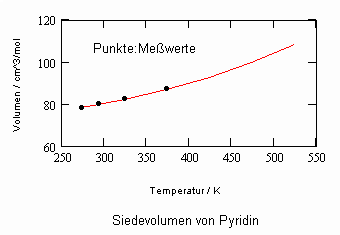
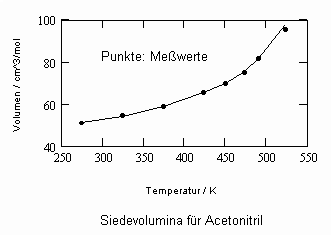
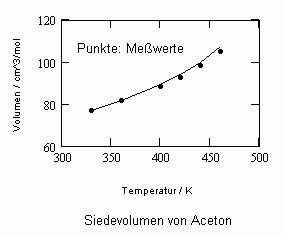
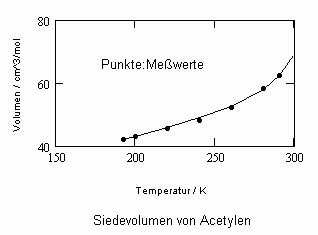
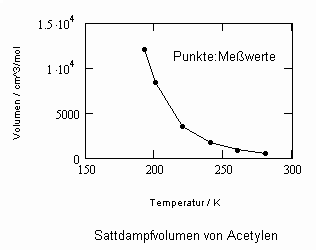
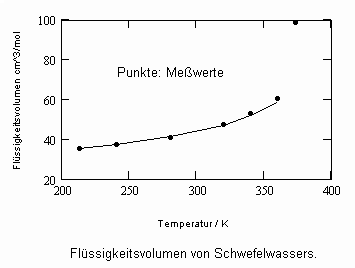
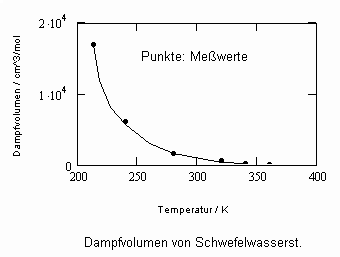
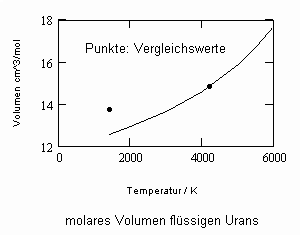
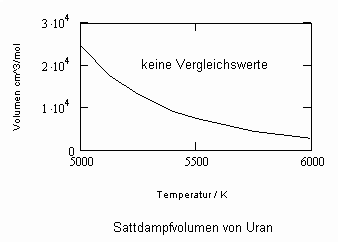
Im Ergebnis der durchgeführten Untersuchungen zeigt sich speziell für Flüssigkeiten, die unter ihrem Dampfdruck bis zu hohen Drücken stehen können, daß das (p,v,T)- Zustandsverhalten von Flüssigkeiten richtig erfaßt werden kann, wenn Gesetzmäßigkeiten kritischer Phänomene auf Zustände weitab vom kritischen Punkt übertragen werden (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“- ISBN 978-3-00-027253-0). Es ist auf solch einer Grundlage möglich, sowohl das Siedevolumen v‘ der Flüssigkeit als auch das Sattdampfvolumen v“ eines Stoffes als Näherung zu berechnen, wobei vor allem die Flüssigkeitswerte erstaunlich gut mit Meßwerten übereinstimmen. Dies alles erweist sich als möglich ohne Voraussetzung einer speziellen Zustandsgleichung bzw. einer empirischen Zustandsgleichung mit Parametern, die durch Anpassung an Meßwerte erst bestimmt werden müssen.
Die Rechenprogramme hierzu liegen vor.
Bei formaler Voraussetzung der klassischen van der Waals- Gleichung als physikalisch begründete Zustandsgleichung
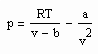
(p- Druck/ MPa, T- Temperatur / K, v- spezifisches Volumen / cm³/mol, b- Eigenvolumen / cm³/mol, a- Parameter / MPa (cm³/mol)²) sind bei vorgegebener Temperatur, bekanntem Dampfdruck ps und den berechneten sich aus der erweiterten Theorie kritischer Phänomene ergebenden Flüssigkeits- und Dampfvolumina v‘ und v“ die Parameter a und b unbekannt bei Voraussetzung dieser Parameter als mit der Temperatur veränderliche Größen. Es bestehen also zwei Unbekannte- nämlich a und b.
Die Verbindung zwischen Flüssigkeits- und Dampfdaten wird durch das Maxwell- Kriterium
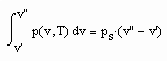
hergestellt.
Es bestehen also zwei Gleichungen für die beiden unbekannten Parameter a, b, die somit bestimmt werden bei Vorgabe der Volumina v‘ und v“, die sich allein mit Gesetzmäßigkeiten kritischer Phänomene berechnen lassen. Die so berechneten Parameter a, b entsprechen keineswegs den mit der klassischen van der Waals- Gleichung benutzten a, b- Werten. Die Unterschiede sind erheblich.
Werden nun die berechneten Parameter a,b der vorausgesetzten o. gen. Zustandsgleichung zu Grunde gelegt, können bei vorgebener Temperatur und vorgegebenem Druck die entsprechenden Flüssigkeitsvolumina bzw. Dichten und die entsprechenden Realgasfaktoren Z = pv/RT selbst bis zu nahkritischen Zuständen berechnet werden. Die Ergebnisse erweisen sich für Volumina durchaus immer in der Nähe der Meßwerte bzw. der aus Meßwerten berechneten Realgasfaktoren. Die dafür erforderlichen Berechnungen liegen programmiert vor. Alle bisher in diesem Blog für Flüssigkeiten gen. Berechnungsergebnisse wurden auf die geschilderte Art und Weise gewonnen. Die Theorie dazu ist aus der Broschüre „Stoffwerte von Flüssigkeiten und realen Gasen -berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0) zu ersehen.
Voraussetzung zur Nutzung der aufgezeigten Berechnungsmöglichkeiten ist allerdings das Vorliegen der kritischen Daten des jeweiligen Stoffes. Aber gerade diese Angaben sind nicht immer bekannt. Trotzdem besteht zumindest für Zustände bei Temperaturen , die niedrigen Dampfdrücken entsprechen, auch bei unbekannten kritischen Daten die Möglichkeit, zu Ergebnissen zu gelangen. Für solche Zustände nämlich vereinfachen sich die Berechnungsgleichungen für die Parameter a und b. Die Daten des kritischen Punktes sind nun nicht mehr zur Berechnung des Parameters a und des Eigenvolumens b erforderlich.
So können also immer z.B. für den normalen Siedepunkt eines Stoffes die Parameter a und b mit diesen vereinfachten Gleichungen berechnet werden, da sich die Daten des normalen Siedepunkts leicht aus den für viele Stoffe vorliegenden Stoffdatensammlungen ergeben oder auch oft einfach durch Messung bestimmbar sind.
Das Eigenvolumen b, das so für Zustände bei Temperaturen niedrigen Dampfdrucks bestimmt wird, hat die äußerst interessante Eigenschaft, über weite Temperaturbereiche fast konstant zu sein. Es variiert nur gering in einem Temperaturbereich des jeweiligen Stoffes bei niedrigen bis mäßigen Dampfdrücken von einigen MPa. Die Theorie und nähere Einzelheiten hierzu sind in der Broschüre „Die Berechnung von Druck- und Volumendaten reiner Stoffe“ (ISBN 3-00-015256-3) dargelegt.
Diese spezielle Eigenschaft der fast bestehenden Konstanz des Eigenvolumens bei Temperaturen niedrigen Dampfdrucks kann zur Berechnung von von (p,v,T)- Daten eines Stoffes sinnvoll ausgenutzt werden. Man braucht nur das Eigenvolumen für einen bekannten Datenpunkt des Dampfdrucks pso, des Siedevolumens v’o und der Temperatur To (z.B. für den normalen Siedepunkt) zu berechnen, um bei anderen Temperaturen, vorgegebenen Druck und dem schon berechneten Eigenvolumen das entsprechende Volumen bzw. die Dichte der Flüssigkeit mit einer speziellen Flüssigkeitszustandsgleichung bestimmen zu können.
Mit dieser speziell für Flüssigkeiten geltenden Zustandsgleichung ist es tatsächlich möglich, bei gegebenem Dampfdruck das Siedevolumen v‘ bzw. bei vorgegebenem Druck (über dem Dampfdruck) das entsprechende Flüssigkeitsvolumen zu berechnen. Damit kann dann auch der Realgasfaktor Z = pv/RT der Flüssigkeit bis zu hohen Drücken bestimmt werden.
Berechnungsbeispiele zur Anwendung der hier für Flüssigkeiten aufgezeigten Möglichkeiten werden in nachfolgenden Artikeln angegeben.
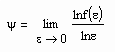
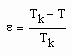 ,
,