Archive for the ‘Berechnung von Dampfdrücken’ Category
Zur Anwendung der Redlich- Kwong- und der Soave- Redlich – Kwong- Gleichung
Freitag, Oktober 13th, 2017Völlig neue Möglichkeiten der Berechnung von pvT- Daten der kritischen Region reiner Stoffe
Sonntag, August 20th, 2017Die Berechnung von Dampfdrücken
Freitag, Dezember 11th, 2009Die Kenntnis des Dampfdrucks einer Substanz ist für chemisch- physikalische und verfahrenstechnische Berechnungen von oft entscheidender Bedeutung. Für viele Stoffe liegen Meßwerte in Abhängigkeit von der Temperatur tabelliert in Stoffdatensammlungen vor. Bei Stoffen aber, die durch Messungen nicht oder nur unvollständig erfaßt sind, ist die Berechnung von Dampfdrücken erforderlich. Ausgangspunkt solcher Rechnungen ist oft die Clausius- Clapeyronsche Gleichung oder auch empirisch aufgefundene Gleichungen- wie z. B. die Antoine- Gleichung oder auch die sogen. Wagner- Gleichung.
Voraussetzung solcher Berechnungen ist immer die Kenntnis wenigstens einiger Meßwerte bei verschiedenen Temperaturen, um so Parameter der vorausgesetzten Dampfdruckfunktion bestimmen zu können. Mindestens zwei Dampfdruck- Meßwerte sind also immer erforderlich, um sinnvoll zwischen den Temperaturen der beiden Meßwerte mit der vorausgesetzten Dampfdruck- Funktion interpolieren zu können.
Mit den in der Broschüre „Die Berechnung von Druck- und Volumendaten reiner Stoffe“ (ISBN 3-00-015256-3) dargelegten Untersuchungen ergibt sich eine völlig neue Möglichkeit. Für einen niedrigen Dampfdruck pso bei der Temperatur To erweist es sich als möglich, die Dampfdrücke bei Temperaturen T in der Umgebung der Temperatur To mit
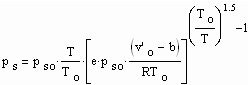 (1)
(1)
als Näherung zu berechnen. Dabei ist v’o das molare Siedevolumen (cm³/mol) des jeweiligen Stoffes bei der Temperatur To. Der Parameter b (cm³/mol) ist das sogen. Eigenvolumen des Stoffes, das mit
![]() (2)
(2)
zu berechnen ist. Der Datenpunkt (pso, To,v’o) kann durchaus der normale Siedepunkt eines Stoffes mit den Angaben für den Druck (0.1013 MPa), die Temperatur und das Volumen sein. Die Größe R ist die allgemeine Gaskonstante (8.314 J/mol K).
Da für sehr viele Stoffe die Angaben zum normalen Siedepunkt durch entsprechende Tabellenwerke oder Datenbanken bekannt sind oder durch Messung einfach zu bestimmen sind, kann das Eigenvolumen immer berechnet werden. Dies bedeutet, Dampfdrücke für Temperaturen etwas unterhalb und oberhalb der normalen Siedetemperatur eines Stoffes können immer mit (1) berechnet werden. Nur ein einziger Datenpunkt (To,v’o) ist dazu erforderlich! Das aber sind leicht zu bestimmende Größen, die durch die Temperaturmessung der siedenden Flüssigkeit und durch die Messung der Dichte einfach zu beschaffen sind.
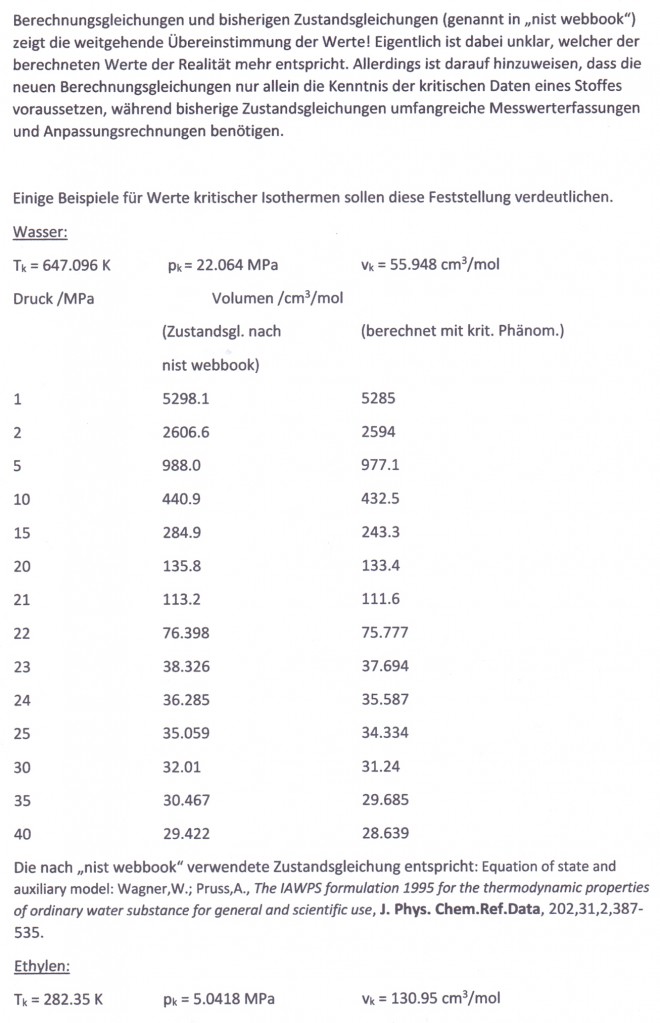
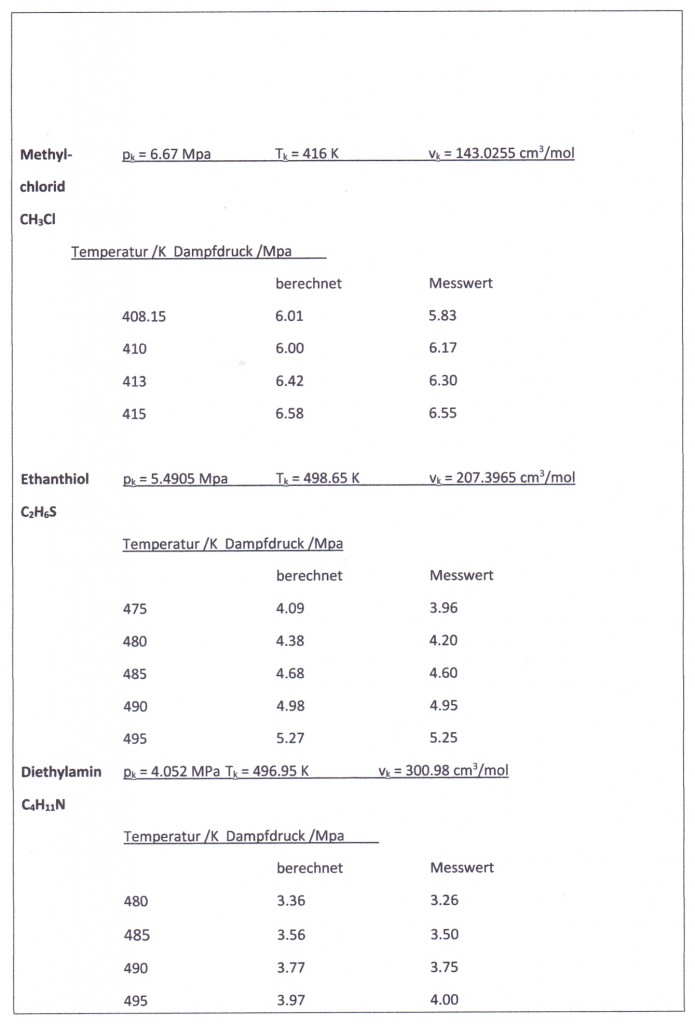
Einige Beispiele sollen die aufgezeigte Berechnungsmöglichkeit für Dampfdrücke verdeutlichen. Für die Stoffe Propylen und Wasser sind in den nachfolgenden beiden Diagrammen die nach (1) und (2) berechneten Dampfdrücke im Vergleich zu den Meßwerten dargestellt, wobei der Ausgangspunkt der Berechnungen die Daten des normalen Siedepunkts sind.
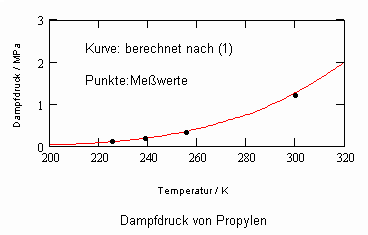
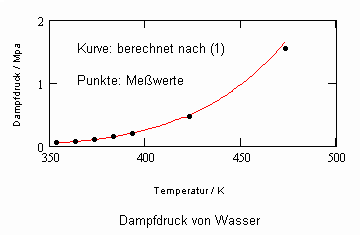
Analoge Rechnungen mit anderen Stoffen belegen immer wieder die Möglichkeit, bei Kenntnis nur des einen Datenpunktes (pso,To, v’o) den Dampfdruckverlauf mit (1) als Näherung in der Umgebung dieses Punktes zu berechnen.
Nicht in jedem Fall ist es möglich, der Empfehlung zu folgen, die Werte des normalen Siedepunktes zur Berechnung des Eigenvolumens zu benutzen. Oftmals ist zwar die normale Siedetemperatur bekannt, nicht aber die dazugehörige Flüssigkeitsdichte. Selbstverständlich kann zur Ermittlung des Eigenvolumens jedes andere bekannte ps,v‘, T- Tripel bei Anwendung von (2) benutzt werden ( es muß nur die Bedingung niedrigen Dampfdrucks eingehalten sein).
Um zu verdeutlichen, daß der Dampfdruckverlauf nach (1) auch für Verbindungen komplizierter chemischer Struktur bestimmt werden kann, sind im nachfolgenden Diagramm die Beispiele
-Butansäuremethylester C5H10O2
-d-Campher C10H16O
-Idryl (Fluoranthen) C16H10O
-Benzanthron C17H10O
angegeben. Das Eigenvolumen dieser Stoffe wurde mit Dampfdruckwerten im Bereich von nur 1 bis 10 Torr, den dazugehörenden Temperaturen und den bei diesen Temperaturen bekannten Flüssigkeitsdichten berechnet. Es ist ersichtlich, das selbst für hochsiedende Verbindungen komplizierter chemischer Struktur die Übereinstimmung zwischen gemessenen und berechneten Dampfdrücken recht gut ist.
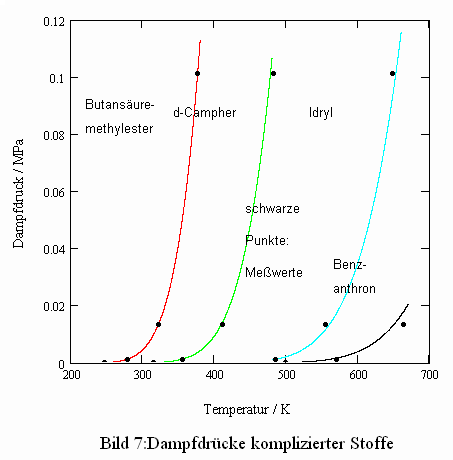
Eine Verbesserung der Genauigkeit bei der Dampfdruckberechnung ist folgendermaßen möglich: Die Basis epso(v’o-b)/RT der Exponentialfunktion in (1) ist eine konstante Größe. Da die Dampfdruckfunktion (1) als eine Näherung nur für niedrige bis mäßige Drücke und entsprechend niedrige Temperaturen weit ab von den kritischen Werten gilt, ist es naheliegend, eine Anpassung der Dampfdruckfunktion (1) an den realen Verlauf bei höheren Drücken durch Einführung einer Temperaturfunktion statt einer Konstanten in der Basis der Exponentialfunktion von (1) vorzunehmen:
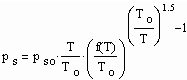 . (3)
. (3)
Die Funktion f(T) ist in eine Reihe f(T) = A+BT+CT²+…… zu entwickeln, die – bei Voraussetzung genügend schneller Konvergenz- schon nach einigen Gliedern abgebrochen werden kann.
Die Koeffizienten A, B, C… sind mit Dampfdruckwerten, die als Meßwerte für bestimmte Temperaturen vorliegen, zu bestimmen. Der Dampfdruckverlauf ist damit innerhalb des Temperaturintervalls, für das Meßwerte vorliegen, mit
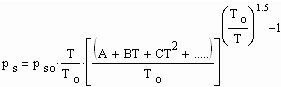 (4)
(4)
als Temperaturfunktion gegeben.
Zwei Beispiele sollen das verdeutlichen.
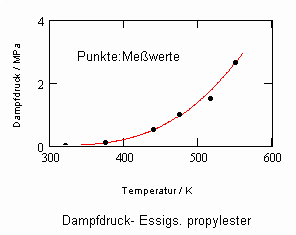
Essigsäurepropylester C5H10O2:
Mit der normalen Siedetemperatur To=375 K, der kritischen Temperatur Tk=549.35 K, dem kritischen Druck pk=2.655 MPa und dem Dampfdruck 0.5065 MPa bei 438.9 K ergibt sich entsprechend (4) eine Dampfdruckfunktion mit zwei Parametern A,B. In dem nachfolgendem Diagramm ist diese Näherungsfunktion des Dampfdrucks im Vergleich mit Meßwerten dargestellt. Die weitgehende Übereinstimmung der Näherung mit Meßwerten ist ersichtlich.
Schwefelwasserstoff H2S
Werden die folgenden Datenpunkte
To=212.8 K (normale Siedetemperatur), T1=240 K, ps1=0.325 MPa, T2=300 K, ps2=2MPa,
T3=373.15 K, ps3=8.937 MPa
zur Bestimmung der Dampfdrucknäherung entsprechend (4) zu Grunde gelegt, entsteht für Schwefelwasserstoff mit 3 Parametern A,B,C das folgende Diagramm:
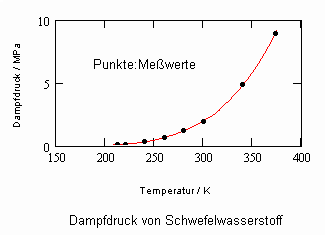
Die weitgehende Übereinstimmumng der Näherungsfunktion nach (4) mit Meßwerten ist auch hier ersichtlich.
Zusammenfassend ist festzustellen:
-In all den Fällen, in denen für einen Stoff nur ungenügende oder keine Meßwerte vorliegen, kann nach Bestimmung zumindest der normalen Siedetemperatur und der entsprechenden Siededichte der Dampfdruck als Temperaturfunktion in der Umgebung der normalen Siedetemperatur mit (1) und (2) als Näherung berechnet werden.
– In all den Fällen, in denen für einen hochsiedenden Stoff nur sehr niedrige Dampfdruckwerte (z. B. im Torr- Bereich) bei den entsprechenden Temperaturen bekannt sind, ist der Dampfdruckverlauf ebenfalls bestimmbar, wenn nur ein Datenpunkt mit den Angaben bei einem niedrigen Druck, der entsprechenden Temperatur und der entsprechenden Flüssigkeitsdichte vorliegt (als Flüssigkeitsdichte kann in diesen Fällen durchaus die Dichte am Schmelzpunkt bzw. Tripelpunkt angesetzt werden).
-Da die mit (1) gegebene Näherung des Dampfdruckverlaufs bei höheren Temperaturen bzw. Temperaturen zunehmend in der Nähe der kritischen Temperatur ungünstiger wird, ist (4) zur näherungsweisen Dampfdruckberechnung eines Stoffes anzuwenden, wenn zumindest einige Meßwerte des Dampfdrucks bei den entsprechenden Temperaturen vorliegen. Die Fehler können klein und vertretbar im Prozentbereich und darunter gehalten werden.