Archive for the ‘Universalitätshypothese’ Category
Neue kritische Exponenten etsprechend der Universalitätshypothese
Dienstag, Januar 1st, 2019Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region
Montag, April 15th, 2013Für technisch wichtige Stoffe existieren heute recht genaue Zustandsgleichungen, die die Variablen Druck p, Temperatur T und Volumen v bzw. die Dichte ρ sowohl im Flüssigkeits- als auch im Gaszustand miteinander verbinden. Da es für die in der verfahrenstechnisch – großtechnischen Praxis bestehenden Anforderungen auf eine hohe Genauigkeit ankommt, reichen Berechnungsgleichungen auf Modellvorstellungen der Theoretischen Physik (auf der Basis der van der Waals- Gleichung und ihren vielen sogen. halbempirischen Weiterentwicklungen, der Virialgleichung usw. bis hin zur sogen. molekularen Thermodynamik) nicht aus. Deshalb müssen immer noch Zustandsgleichungen mit ausgeprägt empirischen und stoffspezifischen Anteilen verwendet werden, um die erforderliche Genauigkeit zu ermöglichen. Der Aufwand ist hoch. Er setzt sehr genaue und umfangreiche pvT- Messungen des jeweiligen Stoffes voraus, um die erforderlichen Anpassungen der experimentell ermittelten Zustandsdaten an Parameter vorausgesetzter Zustandsgleichungen zu ermöglichen. Die Erfolge dieser Vorgehensweise mit weitgehend empirischen und „halbempirischen“ Zustandsgleichungen sind offensichtlich.
Selbst für den die menschliche Existenz begründenden Stoff „Wasser“ sind solch weitgehend empirische Zusammenhänge auf der Grundlage sehr genauer pvT- Messungen entwickelt worden (entsprechend der sogen. IAPWS formulation- „International Association for the Properties of Water and Steam“), keineswegs aber auf der alleinigen Grundlage eines nur physikalisch begründeten Modells. Auch für die wichtigen Stoffe der Erdöl- und Erdgasgewinnung und Verarbeitung- wie z.B. Methan, Ethan……bis Benzol, Toluol usw.- existieren Zustandsgleichungen dieser Art.
Meßwerte vieler Substanzen sind heute in Datenbanken dokumentiert, die einen schnellen Zugriff (allerdings oft gebührenpflichtig) über das Internet gestatten (s. z.B. die umfangreiche Stoffdatensammlung „dechema.de/detherm“). Die Bereitstellung von Stoffdaten geht unterdessen so weit, für eine Vielzahl technisch wichtiger Stoffe komplette pvT-Datensätze und auch kalorische Daten anzugeben (s. „nist webbook“), die nach Vorgabe von Druck und Temperatur entsprechend der jeweiligen Dichte bzw. des Volumens mit einer weitgehend an Meßwerte angepaßten Zustandsgleichung ermittelt wurden- und das sowohl für die flüssige Phase und auch für die Gasphase und überkritische Zustände. Die Fehler dabei sind durchaus gering und liegen oft nur im Prozentbereich oder sogar darunter. Sie sind so geeignet für verfahrenstechnische Auslegungen großtechnischer Prozesse mit solchen Stoffen.
Dies alles trifft zu nur für pvT- Zustände weiter entfernt von den kritischen Daten. Soll bei Vorgabe von Druck und Temperatur in einem nahkritischen Bereich die Dichte bzw. das Volumen eines Stoffes mit einer solchen Zustandsgleichung bestimmt werden (dokumentiert z.B. in „nist webbook“) ist das zwar möglich- die Fehler aber werden dann oft als „höher“ im Vergleich zu den Fehlern angegeben, die in Zuständen weiter entfernt von den kritischen Daten festgestellt sind. So heißt es dann z.B. bei nist webbook für Ammoniak: „The uncertainties of the equation of state are o.2% in density….., except in the critical region“.
Und so etwa lauten ähnliche Feststellungen für auch ander Stoffe:
– „Uncertainties will be higher near the critical point“- nist webbook für H2S
– „In the critical region the uncertainties are higher for all properties, except vapor pressure“- nist webbook für SO2.
Die Liste von Stoffen mit der Aussage „except in the critical region“ zu den in der Literatur angegebenen Zustandsgleichungen kann fortgesetzt werden, z. B. mit solchen grundlegenden und strukturell einfachen Stoffen wie Pentan, Propylen, Methan u.a. So ist also die Feststellung gerechtfertigt, dass die Ungenauigkeiten bisheriger veröffentlichter Zustandsgleichungen speziell in der kritischen Region selbst nach den durchgeführten sehr genauen pvT-Messungen und Anpassungen immer noch recht hoch sind. Der Aufwand ist hoch in Relation zum Ergebnis.
Die Hoffnung, dass sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Nun hat es sich aus theoretischen Erwägungen zur Physik kritischer Phänomene ergeben, einen anderen als bisherige Ansätze zur Auswertung dieser Phänomene zu verfolgen.
Das bisherige Theorie- Ergebnis ist, dass man bei Kenntnis nur der kritischen Daten eines Stoffes weitgehend zutreffende Näherungsaussagen zum pvT- Verlauf der kritischen Isotherme bzw. von nahkritischen Isothermen erhalten kann- ohne zusätzliche Meßwerte. Für Stoffe also, zu denen keine weiteren Messungen außer denen der kritischen Daten vorliegen, können dann zumindest Näherungen des Isothermen -Verlaufs in der kritischen Region abgeleitet werden. Da das für sehr, sehr viele Stoffe zutrifft, ist es also durchaus möglich, die Daten der kritischen Isotherme und auch pv-Daten etwas unterhalb und oberhalb der kritischen Temperatur als Näherung zu berechnen. Nähere Ausführungen zur Theorie und zu Beispielrechnungen sind im Artikel vom 1.7.12 in www.dr-tampe.de u.a. enthalten.
Bisher war es nicht möglich, die Sättigungsvolumina der siedenden Flüssigkeit und des Sattdampfes für Temperaturen kurz unter der kritischen Temperatur vorauszuberechnen. Mit den neuen Theorie- Ergebnissen zu kritischen Phänomenen erweist sich das unterdessen als möglich. Die berechneten Volumina sind Näherungen, die durchaus weitgehend mit Meßwerten übereinstimmen (s. Artikel“ Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur“ in www.dr-tampe.de .)
Zur Berechnung nahkritischer Stoffdaten von Flüssigkeiten und Gasen
Sonntag, Juli 1st, 2012Aus der physikalischen Theorie kritischer Phänomene kann für reale Gase die Zustandsfunktion
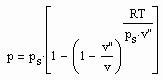(1)
für Zustände entfernt vom kritischen Punkt bzw. für kleine bis mäßige Drücke abgeleitet werden (p- Druck/ MPa, ps- Dampfdruck/ MPa, T- Temperatur / K, v- molares Volumen / cm³/mol, v“- molares Sattdampfvolumen / cm³/mol ). Die Funktion (1) ist als grobe Näherung anwendbar. Sie ist anwendbar auch für hohe Temperaturen, sogar bis über die kritische Temperatur hinaus. Ihre Anwendbarkeit für Zustände nahe des kritischen Punktes ( einige Kelvin unterhalb und oberhalb der kritischen Temperatur Tk und für Drücke in der Nähe des kritischen Druckes pk ) ist nicht zu erwarten, da hier besondere und andere Bedingungen gelten, die sich aus Gesetzmäßigkeiten kritischer Phänomene im Unterschied zur bisherigen van der Waals- Thermodynamik ergeben.
Auf der kritischen Isotherme können entsprechend der Gesetzmäßigkeiten kritischer Phänomene nahe des kritischen Druckes die Relationen
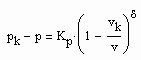(2)
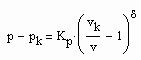(3)
vorausgesetzt werden. Dabei ist Kp ein Proportionalitätsfaktor und δ der entsprechende kritische Exponent. (2) gilt für p ‹ pk , (3) gilt für p › pk.
Für p,v – Zustände nahe pk, vk ist (2), (3) zwingend mit einem in der Theorie kritischer Phänomene erklärten kritischen Exponenten zu rechnen. Der kritische Exponent δ ist resultierend aus Messungen in der Größenordnung von 4.0 bis 4.8 festgestellt worden (s. z. B. Nolting, W.: Statistische Physik, Springer Verlag 2004). Es gibt Physiker, die kritische Exponenten im Sinne absoluter Naturkonstanten unabhängig vom Stoff interpretieren und andere, die eine Stoffabhängigkeit in Grenzen zugestehen. Setzt man die weitgehende Stoffunabhängigkeit voraus, verbleibt der Proportionalitätsfaktor Kp als Unbekannte. Es besteht die Frage, wie ist der Proportionalitätsfaktor Kp zu bestimmen, um Zustände auf der kritischen Isotherme berechnen zu können?
Sinnvoll ist es, die Frage allgemeiner zu stellen. Nämlich: Wie können nahkritische Zustandsdaten mit ausreichender Genauigkeit nicht nur für Zustände auf der kritischen Isotherme, sondern auch für Temperaturen kurz unter- und oberhalb der kritischen Temperatur bestimmt werden? Bisherige physikalisch begründete als auch die sogen. halbempirischen Zustandsgleichungen u.a. reichen nicht aus. Auch die von der bisherigen Theoretischen Physik erklärten Ansätze, die die rechnerische Bestimmung des Proportionalitätsfaktors Kp ohne Meßwerte kaum erlauben, reichen nicht aus. Für technisch wichtige Stoffe ist deshalb die Physikalische Chemie und Verfahrenstechnik auf empirische stoffspezifische Lösungen bei einem hohen meßtechnischen Aufwand angewiesen (vielparametrige empirische Zustandsgleichungen pro Stoff bei Voraussetzung hochgenauer Stoffwerte) ( s. z. B. die Stoffdaten für Erdgaskomponenten, für Kohlenstoffdioxid CO2, für Wasser usw. mit weitgehend empirischen Zustandsgleichungen von Wagner und Span, Universität Bochum, s. E.W. Lemmon u. R. Span: Multiparameter Equations of State for Pur Fluids and Mixtures. Chapter 12, in A.R.H. Goodwin, J.V. Sengers und C.Peters(Ed.): Applied Thermodynamics of Fluids. International Union of Pure and Applied Chemistry, Royal Society of Chemistry, Thomas Graham House,Cambridge, UK 2010)).
Bisherige Feststellungen und Schätzungen kritischer Exponenten für dreidimensionale physikalische Systeme mit einem Ordnungsparameter in der entsprechenden Universalitätsklasse wurden z. B. in Auswerung des Issing – Modells mit dem kritischen Exponenten β = 0.326 + – 0.002 und δ = 4.80+- 0.02 vorausgesetzt (s. z. B. J.V. Senger: Thermodynic Behavior of Fluids near the critical Points, Ann. Rev. Phys.Chem. 1986,37).
Vorliegende Ergebnisse zu Gesetzmäßigkeiten kritischer Phänomene bestätigen zwar die Existenz des kritischen Exponenten β in der Größenordnung von 1/3, nicht aber die Gültigkeit eines allgemeinen Exponenten δ etwa bei 4.8. Das in der Theoretischen Physik gen. Werteintervall δ = 4.0 bis 4.8 trifft zu und ist nach den vorliegenden Untersuchungen durchaus noch zu klein.
Die nachfolgenden Feststellungen weisen darauf hin, daß es möglich ist, einen physikalisch begründeten und empiriefreien Ansatz zur Nachrechnung nahkritischer Daten ohne zusätzlichen Meßaufwand zu finden.
Bestimmt man für die kritische Isotherme vergleichsweise für verschiedene Stoffe den Exponenten RTk/pk vk in (1), ist festzustellen: Es gibt Stoffe, deren Exponent RTk/pk vk in (1) in dem für den kritischen Exponenten δ erklärten Bereich zwischen 4.0 bis 4.8 liegt. Für Wasser z. B. ergibt sich 4.36, für Ammoniak NH3 4.12. Für solche Stoffe ist die weitgehende Gültigkeit der Funktion (1) auch im nahkritischen Bereich zu erwarten. Die kritische Isotherme sollte in diesen Fällen entsprechend (1) mit
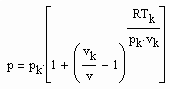v‹ vk (4)
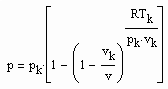v›vk (5)
erfaßt werden können.
Ob das tatsächlich so ist, zeigt die Nachrechnung mit Daten gut vermessener Stoffe wie z. B. für Wasser.
Wasser: (Tk= 647.15 K, pk= 22.055 MPa, vk= 55.9503 cm³/mol)
Bei einer Temperatur 648.15 K (375 °C, also 1°C über der kritischen Temperatur) und einem hypothetischen Dampfdruck von 22.286 MPa ergeben sich mit den o. gen. Funktionen (4), (5) im Vergleich mit aus Meßwerten berechneten Realgasfaktoren die folgenden Werte (außerdem sind die Werte angegeben, die sich mit einer der oft angewendeten Ingenieurgleichungen, der Soave- Redlich- Kwong- Gleichung berechnen lassen).
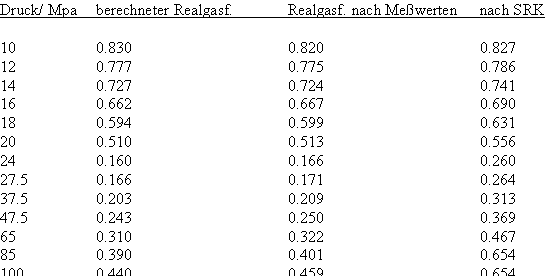
(Meßwerte L. Haar, J.S. Gallagher, G.S. Kell: NBS/NRC Wasserdampftafeln, Springer 1988)
Ein weiteres für die kritische Isotherme vermessenes und veröffentlichtes Beispiel ist
Schwefelhexafluorid SF6: (Tk= 318.7232 K, pk= 3.755 MPa, vk= 196.576 cm³/mol)
Bei einer Temperatur genau auf der kritischen Isotherme ergeben sich mit den o.gen. Funktionen (4), (5) im Vergleich mit aus Meßwerten berechneten Realgasfaktoren die folgenden Werte:
Die gen. Beispiele u.a. zeigen die Anwendbarkeit der Funktionen (4), (5) für kritische Verhältnisse.
Für Stoffe allerdings, deren Exponent RTk/ pk vk nicht in das von der physikalischen Theorie erklärte Wertebereich von ca. 4.0 bis 4.8 für kritische Exponenten fällt, bestehen andere Bedingungen. Allerdings ergibt sich auch für solche Stoffe die Möglichkeit, nahkritische Stoffdaten rechnerisch zu bestimmen. Es ist dazu nur die Kenntnis der kritischen Daten und die vorausgesetzte Temperatur ohne weitere Meßwerte erforderlich.
Die so feststellbare Zustandsfunktion p = p(T,v) gestattet dann auch die Berechnung kalorischer Größen- wie auch der wichtigen Freien Enthalpie für nahkritische Zustände.
Die vorliegenden Theorie – Ergebnisse sollen veröffentlicht werden.
Die sich aus der Theorie kritischer Phänomene ergebenden Weiterentwicklungen ermöglichen es, allgemeine Aussagen zum pvT- Verhalten von Flüssigkeiten abzuleiten. Es ergibt sich eine Zustandsfunktion speziell für Flüssigkeitenvon niedrigen Temperaturen bis hin zu Temperaturen nahe der kritischen Temperatur. Damit kann bei vorgegebener Temperatur und vorgegebenem Druck das molare Volumen einer Flüssigkeit als Näherung selbst bis zu hohen Drücken von einigen 10 MPa und höher berechnet werden, wenn nur die kritischen und die Sättigungsdaten des jeweiligen Stoffes bekannt sind. Die Berechnung der Realgasfaktoren von Flüssigkeiten bis zu hohen Drücken ist somit bei guter Übereinstimmung mit Meßwerten möglich.
Für Flüssigkeitszustände bei Temperaturen niedriger bis mäßiger Dampfdrücke, d.h. weiter entfernt vom kritischen Punkt des jeweiligen Stoffes, ist mit den Mitteln der van der Waals- Thermodynamik die Zustandsfunktion
(6)
ableitbar (b- Eigenvolumen der Moleküle des Stoffes/ cm³/mol, K-stoffspezifische Konstante mit der Dimension eines Druckes, die sich aus dem Dampfdruck ergibt) (s. Tampe,F.: Stoffwerte von Flüssigkeiten und Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene, 2009, ISBN 978-3-00-027253-0).Auch diese Funktion ermöglicht die Berechnung der Flüssigkeitsvolumina als Näherung für Drücke vom Dampfdruck bis weit darüber hinaus- z.B. für Wasser sogar bis 100 MPa. Mit dieser Funktion (6) und der aus der physikalischen Theorie kritischer Phänomene ableitbaren Zustandsfunktion für Flüssigkeiten nahe kritischer Werte ist die Berechnung von Flüssigkeitsdaten als Näherung in ihrem gesamten Existenzbereich von niedrigen bis zu hohen Temperaturen, vom Dampfdruck bis zu hohen Drücken möglich.
Die in der Technischen Thermodynamik , Physikalischen Chemie und Verfahrenstechnik bestehenden Ansätze, Stoffeigenschaften mit den Mitteln der bisherigen van der Waals- Thermodynamik, der Statistischen Thermodynamik mit Mitteln von Potential- Ansätzen der Quantenmechanik bzw. der sogen. molekularen Modellierung zu bestimmen, erweisen sich oft als kompliziert und empiriebelastet. Als viel einfacher gestalten sich die aus Gesetzmäßigkeiten kritischer Phänomene ableitbaren Berechnungsgleichungen, die nicht einmal Anpassungsrechnungen an vorausgesetzte empirische Parameter verlangen.
Weitere Beispiele zu Rechenergebnissen im Vergleich zu Meßwerten können die Anwendbarkeit der gewonnenen Theorie – Ergebnisse, die Näherungen der entsprechenden Stoffwerte erlauben, verdeutlichen: s. Anlage.
Oftmals sind Meßwerte des nahkritischen Sättigungszustandes von Stoffen unbekannt. Die Berechnung solcher Daten für Flüssigkeits- und Dampfvolumina bzw. für Dampfdrücke in der Nähe der kritischen Temperatur ist mit den gegenwärtig verfügbaren Berechnungsgleichungen (van der Waals- Gleichung, sogen. halbempirische Gleichungen nach Soave, Redlich, Kwong und Peng, Robinson u. a., Gleichungen der Statistischen Thermodynamik usw.) in vielen Fällen nicht möglich bzw. zu ungenau.
In Auswertung von Gesetzmäßigkeiten kritischer Phänomene ergibt sich nun die Möglichkeit, nahkritische Sättigungsvolumina bzw. die nahkritischen Dichten von Stoffen für Flüssigkeit und Dampf im Sättigungszustand in Abhängigkeit von der Temperatur zu berechnen. Die Berechnungsgleichungen dafür liegen vor. Die Ergebnisse sind Näherungen, die für den Flüssigkeitszustand sogar besser sind als für den Sattdampf (s. auch Artikel „Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur“ vom 22.2.2011 in www.dr-tampe.de )
Auf Folgendes ist hinzuweisen: Wenn die Zustandsfunktion p= p(v,T) eines Stoffes sowohl sowohl für den Flüssigkeits- als auch für den Gaszustand bekannt ist, muß es möglich sein, kalorische Daten dieses Stoffes zu berechnen. Zur Berechnung z.B. der für technische Belange wichtigen Enthalpie gilt
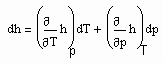. (7)
Da
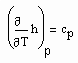(8)
die spezifische Wärmekapazität ist, die gemessen werden kann, und für
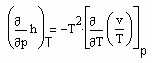(9)
gilt, ist damit die Enthalpie eines Stoffes sowohl für den Flüssigkeitszustand als auch den Gaszustand berechenbar. Dies bedeutet weiter, daß so die Enthalpie eines Stoffes entlang der Dampfdruckkurve sowohl für die Flüssigkeit als auch für den Sattdampf als Näherung berechnet werden kann.
Anlage: Berechnungsbeispiele
Gedanken zur Universalitätshypothese kritischer Phänomene
Sonntag, Dezember 18th, 2011Die in diesem Blog gen. und in einzelnen Artikeln beschriebenen neuen Möglichkeiten der Berechnung thermophysikalischer Daten von Flüssigkeiten und Gasen wurden durch eine Erweiterung der für nahkritische Zustände geltenden Gesetze kritischer Phänomene auf vom kritischen Punkt weit entfernte Zustände gewonnen.
Kritische Phänomene sind in einem engen Bereich der Temperatur oder des Drucks nahe der kritischen Daten untersucht und mit ihren kritischen Exponenten erklärt (s. Artikel vom 1.5.2009 „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ und die Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ – ISBN 978-3-00-027253-0) . In der physikalischen Literatur ist die Wirkung kritischer Phänomene auf Zustandsdaten von Stoffen begrenzt auf sehr nahkritische Verhältnisse- bis einige wenige Kelvin der Temperatur T unter bzw. über der kritischen Temperatur Tk oder nur nahe am kritischen Druck pk. So z. B. heißt es: „Man spricht von kritischen Phänomenen. Ihre Universalität erklärt das heftige Interesse an diesen Phänomenen, obwohl sie sich nur im Bereich der kritischen Fluktuationen, also in einem nur sehr schmalen Temperaturbereich abspielen.“ (Nolting: Grundkurs Theoretische Physik 6, Statistische Physik, Springer 2004.)
Mit den vorliegenden Ergebnissen zumindest für die kritischen Phänomene
– Dichtesprung ρ‘-ρ“ zwischen flüssiger und dampfförmiger Phase im Sättigungszustand
– Differenz vom Druck p zum kritischen Druck pk bzw. von der Dichte ρ zur kritischen Dichte ρk auf der kritischen Isotherme Tk
scheint das aber nicht so zu sein!
Denn es zeigt sich, daß die Proportionalitäten zwischen der Dichtedifferenz ρ‘-ρ“ und (Tk-T)^β (für T<Tk) bzw. p-pk und sign(ρ-ρk)(⁄ρk-ρ⁄)^δ keineswegs nur in der unmittelbaren Nähe des kritischen Punktes gelten. Der Beleg dafür ist die Anwendbarkeit der Gleichungen
und
,
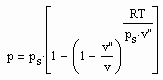die ja erst durch die Erweiterung der gen. beiden kritischen Phänomene auf weit von der kritischen Temperatur entfernte Temperaturen gewonnen werden konnten (ps- Dampfdruck, Kv- sogen. Dichtesprungfaktor), (s. o. gen. Artikel vom 1.5.2009 ). Die gen. beiden Gleichungen gelten trotz ihrer Ableitung aus Gesetzmäßigkeiten kritischer Phänomene keineswegs nur in der unmittelbaren Nähe des kritischen Punktes eines Stoffes. Sie können- wie in den verschiedenen Artikeln dieses Blogs aufgezeigt- durchaus zur näherungsweisen Berechnung von Stoffdaten benutzt werden. Die physikalische Theorie hierzu und die Ableitung dieser und weiterer Gleichungen ist in der o.gen. Veröffentlichung ausführlich dargelegt.
Entsprechend der Universalitätshypothese von Griffiths (R.B. Griffiths, Phys. Rev. Lett. 24, 1479 (1970)) haben die kritischen Exponenten für völlig verschiedene Stoffe fast die gleichen Werte (s. z. B. Nolting: „Grundkurs Theoretische Physik 6, Statistische Physik“, Springer Verlag 2004). Diese sehr erstaunliche Eigenschaft der verschiedensten Stoffe trifft zu- aber eben doch nur fast!
Theoretische Physiker erklären die Universalitätshypothese als unterdessen bewiesen entsprechend der Renormierungsgruppentheorie von K. Wilson.
Damit ist letztlich gesagt, daß die Universalitätshypothese selbst für Stoffe komplizierter chemischer Strucktur zutreffen muß- also nicht nur für Stoffe einfacher Moleküle (wie N2,O2, Ar, He, H2 usw.), für die die meisten Messungen vorliegen, sondern auch für Stoffe größerer Molekülmasse mit z.B. C- Doppelbindungen, aromatischen Ringen, Heterocyclen und der ungeheuren Vielzahl weiterer anorganischen und organischen Verbindungen.
Die Frage,ob das angesichts der überwältigenden Vielfalt von Stoffen immer so entsprechend der Universalitätshypothese tatsächlich ist ( sie selbst formuliert die Einschränkung „fast“ ), muß wohl erlaubt sein. Denn es ist zu bedenken, daß notwendige Untersuchungen und Messungen mit geringer Fehlertoleranz in der Nähe des kritischen Punktes schwierig sind. Nur für relativ wenige Stoffe liegen z.B. p,v- Messungen auf der kritischen Isotherme vor.
Wenn die Universalitätshypothese von einer nur „fast“ zutreffenden Universalität der kritischen Exponenten spricht, ist offensichtlich eine Variabilität dieser Exponenten im Rahmen der Vielfalt unterschiedlicher Stoffe zugelassen. Es ist zu fragen, ob für diese Variabilität die Ungenauigkeit der schwierigen Messung verantwortlich ist oder ob der jeweilige kritische Exponent doch etwas vom Stoff abhängig ist. Auch Nachfragen dazu bei namhaften theoretischen Physikern konnten diese Frage nicht völlig klären. Teilweise wurde auf immer feste Werte der kritischen Exponenten verwiesen, teilweise wurde die Variabilität bei komplizierteren Molekülen und bei veränderten sogen. Universalitätsklassen benannt.
Keineswegs ist es so, daß die Variabilität kritischer Exponenten nur klein ist. Sehr deutlich zeigt sich das an dem kritischen Phänomen,welches den nahkritischen Zusammenhang von Druck und Dichte auf der kritischen Isotherme beschreibt. Für den dazu in der physikalischen Literatur benannten kritischen Exponenten δ wird immerhin ein beträchtlicher Wertebereich von 4 bis 4.8 genannt. Eine weit geringere Streuung der festgestellten Werte des kritischen Exponenten besteht für das kritische Phänomen, das den nahkritischen Dichteverlauf in Abhängigkeit von der Temperatur mit dem in der physikalischen Literatur bezeichneten Exponenten β beschreibt. Die Werte für β streuen nur von 0.33 bis 0.37. Obwohl der versuchstechnische Nachweis und die Gültigkeit des mit dem kritischen Exponenten β verbundenen kritischen Phänomens der Proportionalität der Dichtedifferenz ρ‘-ρ“ mit der Temperaturdifferenz entsprechend (Tk-T)^β nur für Temperaturen in unmittelbarer Nähe der jeweiligen kritischen Temperatur erklärt ist, ergab sich der Nachweis dafür, daß die gen. Proportionalität auch für Zustände weit entfernt von der kritischen Temperatur gilt. Der Ausdruck dafür ist die bereits o. gen. Gleichung
,
die die Grundlage wesentlicher Stoffdatenberechnungen der Artikel dieses Blogs und der Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen – berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0) ist. Wirklich interessant ist, daß diese Gleichung , obwohl sie eigentlich nur für jeweils sehr nahkritische Temperaturen gelten dürfte, tatsächlich für die verschiedensten Stoffe auch komplizierten Molekülaufbaues sehr weit entfernt von der kritischen Temperatur anwendbar ist. Die Frage, warum das so ist , ist letzlich von der heutigen Theoretischen Physik unbeantwortet.
Die Theorie kritischer Phänomene erklärt die Eigenschaften bestimmter physikalischer Größen als eine Reihenentwicklung der reduzierten Temperatur (Tk-T)/Tk. Auch für die Dichtedifferenz ρ‘-ρ“ besteht solch eine Reihenentwicklung. Damit ist es dann möglich, eine sehr genaue Gleichung zur Bestimmung der Siededichte eines Stoffes als Temperaturfunktion abzuleiten, wenn nur einige wenige Meßwerte dazu vorliegen (s. den Artikel vom 5.7.2010 in diesem Blog “ Kritische Exponenten als mögliche Grundlage sehr genauer Stoffwertberechnungen“). Beispielrechnungen bei hoher Übereinstimmung mit Meßwerten wurden mit dem kritischen Exponenten β = 1/3 durchgeführt.
Die o.gen. Zustandsfunktion
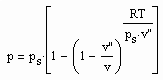
wurde mit einer Erweiterung des für den Druck und der Dichte auf der kritischen Isotherme geltenden kritischen Phänomens des Exponenten δ = 4.4±0.4 abgeleitet. Voraussetzung dabei ist die Hypothese, daß das für die kritische Isotherme erklärte kritische Phänomen
(const- Konstante) auf Drücke weit entfernt vom kritischen Druck und auch auf Temperaturen entfernt von der kritischen Temperatur übertragen werden kann. Die mathematische Strucktur der sich mit dieser Hypothese ergebenden Gleichungen führt dann allerdings nicht zu dem Exponenten δ, sondern zu einem Exponenten RTk/pkvk für die kritische Isotherme bzw. zu RT/psv“ für eine von Tk verschiedene Temperatur.
Interessant ist, daß dieser sich aus der Rechnung ergebende Exponent der reziproke Wert des in der Technischen Thermodynamik verwendeten Realgasfaktors eines Gases im Sättigungszustand ist: ps v“/RT. Auf der kritischen Isotherme liegen Werte des reziproken Realgasfaktors für alle möglichen Stoffe oft bei 3.5 bis 4.5- also durchaus in der Größenordnung des kritischen Exponenten δ= 4.4±0.4. Wenn bedacht wird, daß der kritische Exponent um 4.4 nur auf der kritischen Isotherme in der unmittelbaren Nähe des kritischen Drucks gilt, ist der Unterschied zum reziproken Wert des Realgasfaktors evtl. durch die Erweiterung des kritischen Phänomens auf Drücke keineswegs nur in der Nähe des kritischen Drucks erklärbar. Die näherungsweise Gültigkeit der abgeleiteten o. gen. Zustandsfunktion ist durch eine Vielzahl von Nachrechnungen bei Vergleichen mit Meßwerten nachgewiesen. Sie hat den Vorteil, unabhängig von empirischen Voraussetzungen zu sein- z. B. von dem in der Technischen Thermodynamik für sogen. halbempirische Zustandsgleichungen notwendigen völlig empirischen azentrischen Faktor.
Die bisherigen Untersuchungen zur Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene auf Daten weiter entfernt von Daten des kritischen Punktes sind bisher nur auf die o.gen. kritischen Phänomene bezogen. Ergebnisse zur Kompressibilität und vor allem zur der Wärmekapazität eines Stoffes als Funktion der Temperatur liegen noch nicht vor; sie sind in Arbeit, um festzustellen, ob auch dafür Gesetzmäßigkeiten kritischer Phänomene im beschriebenen Sinne modifiziert werden können.