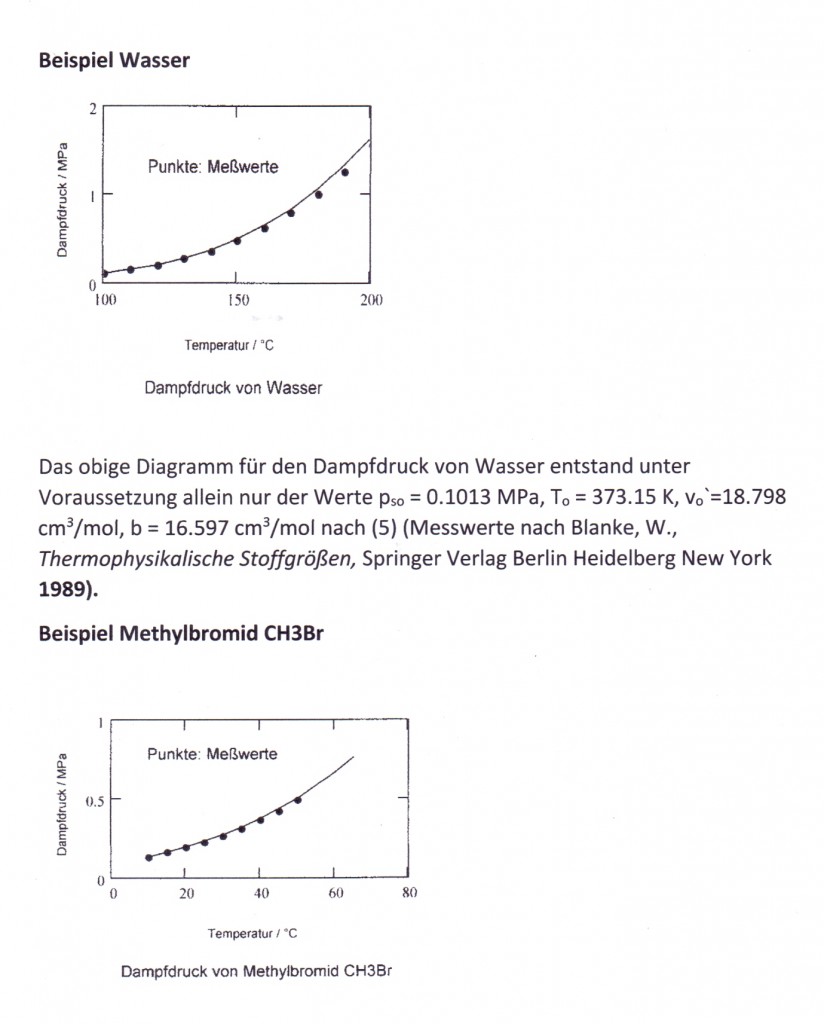
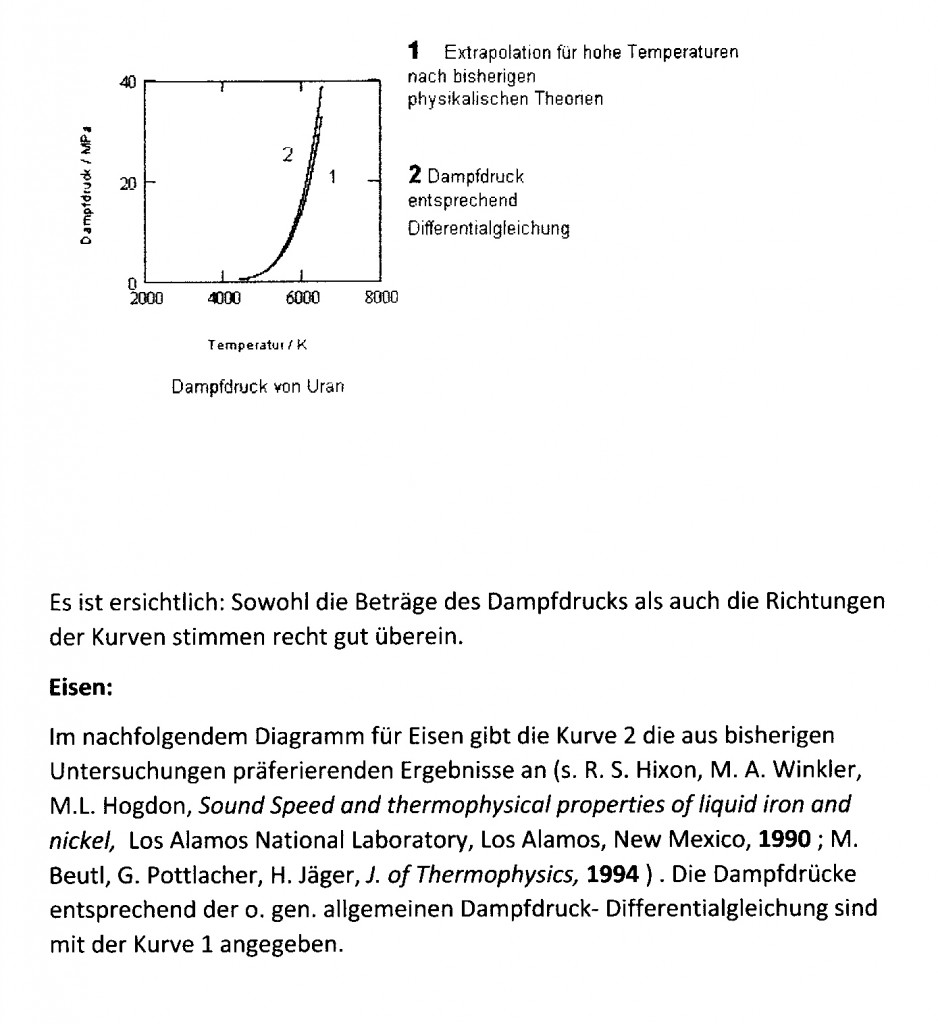
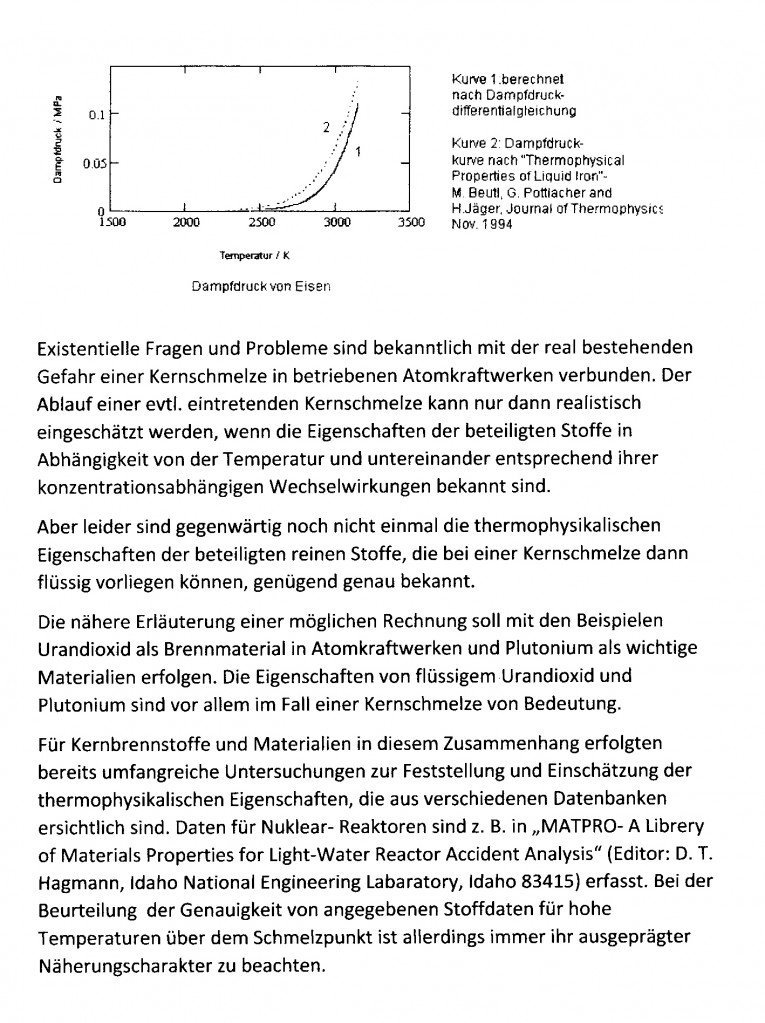
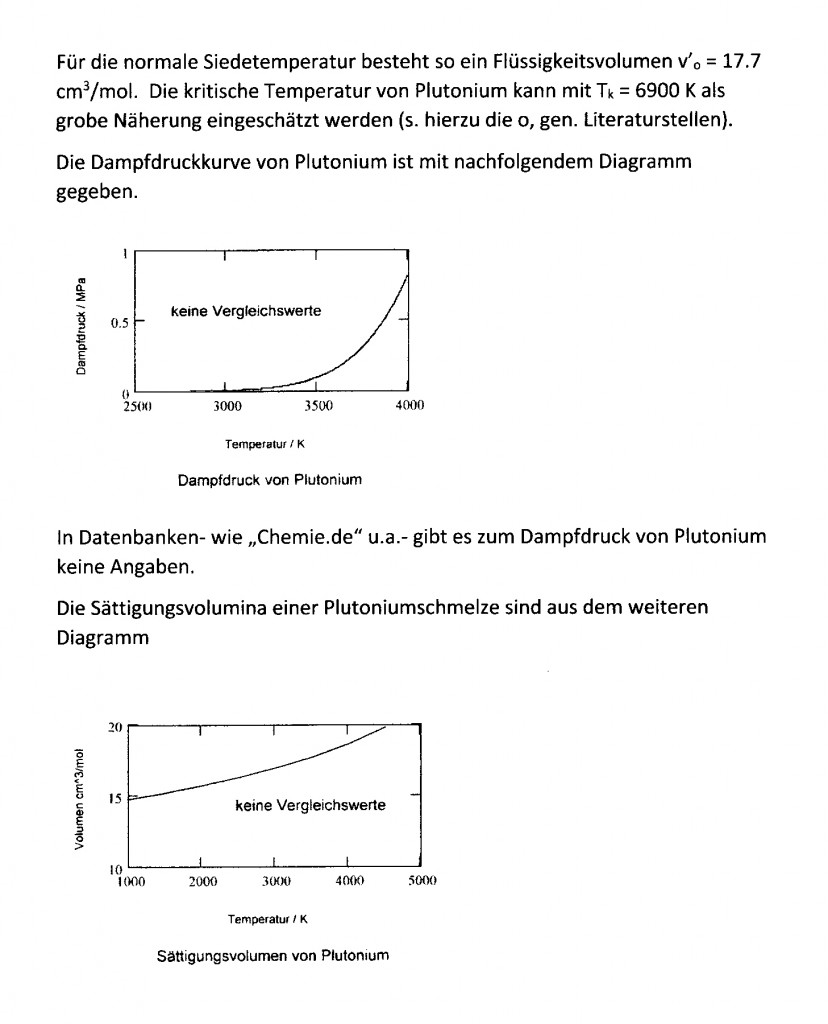
Archive for the ‘Thermodynamik’ Category
Zur Anwendung der Redlich- Kwong- und der Soave- Redlich – Kwong- Gleichung
Freitag, Oktober 13th, 2017Die Auswertung und Anwendung kritischer Phänomene der Theoretischen Physik
Dienstag, Juni 16th, 2015Die Bestimmung der Stoffeigenschaften von Flüssigkeiten und Gasen in der kritischen Region eines Stoffes ist mit besonderen Schwierigkeiten verbunden. Die Ursache dieser Schwierigkeiten ist letzlich das Eintreten kritischer Phänomene, die in der kritischen Region nicht den klassischen van der Waals- Teilchenwechselwirkungen entsprechen. Auf neue sich aus der physikalischen Theorie kritischer Phänomene ergebende Möglichkeiten ist hinzuweisen. Sie ergeben sich u. a. aus Untersuchungen zur Festlegung kritischer Exponenten mit völlig neuen Ergebnissen. Es zeigt sich auf der Grundlage dieser neuen Möglichkeiten, daß nun pvT- Daten auch im kritischen Gebiet mit erfreulicher Genauigkeit nur durch Rechnung wiedergegeben werden können. Das betrfft die pv- Werte auf der kritischen Isotherme und auf Isothermen unterhalb und oberhalb nahe der kritischen Temperatur und auch Näherungen für die unterhalb der kritischen Temperatur bestehenden Sättigungsvolumina v′, v′′ für Flüssigkeit und Dampf.
Da die Vermessung von pvT- Daten in den kritischen Bereichen von Stoffen schwierig, aufwändig und teuer ist, gibt es gar nicht so viele aus Stoffdatenbanken abrufbare Ergebnisse. Allerdings sind z. B. in der web-site „nist webbook“ für etliche technisch wichtige Stoffe Ergebnisse mit den wahrscheinlich gegenwärtig am besten geeigneten überwiegend empirischen Zustandsgleichungen mit „Java“ abrufbar. Auch für die jeweilige kritische Region geben die in „nist webbook“ verwendeten Zustandsgleichungen pvT- Daten an. Allerdings betonen die verschiedenen Autoren immer wieder die Feststellung: „The Uncertainties are higher….“. Trotz der labortechnisch mit Aufwand erfaßten Stoffdaten besteht die Einschätzung, daß mit den verwendeten weitgehend empirischen herkömmlichen Zustandsgleichungen im kritischen Gebiet die Realität mit nur größeren Fehlern beschrieben wird.
Sehr interessant ist nun ein Vergleich der Ergebnisse, die sich für die kritische Isotherme eines Stoffes mit den neuen sich aus der physikalischen Theorie kritischer Phänomene abgeleiteten Gleichungen und den bisherigen weitgehend empirischen Zustandsgleichungen ergeben. Es zeigt sich die in der Größenordnung der Werte weitgehende Übereinstimmung. Eigentlich ist dabei unklar, welcher der berechneten Werte der Realität mehr entspricht. Allerdings ist auf einen sehr wichtigen Unterschied hinzuweisen: Die neuen aus der physikalischen Theorie kritischer Phänomene folgenden Gleichungen benötigen nur allein die Kenntnis der kritischen Daten eines Stoffes, während bisherige Zustandsgleichungen neben zusätzlichen Meßwerterfassungen auch in der kritischen Region außerdem noch Anpassungsrechnungen der Meßwerte an die vorausgesetzte Zustandsgleichung erfordern.
Ergebnisse der Berechnung von Volumina auf der kritischen Isotherme eines Stoffes oder in ihrer Nähe bei vorgegebenem Druck sind bereits als Beispiele für etliche Stoffe in Artikeln dieses Bloggs im Vergleich zu Werten mit herkömmlichen empirischen Zustandsgleichungen genannt (s. z. B. Berechnungen des Verlaufs kritischer Isothermen/ September bis Oktober 2014 für Propylen, Wasser, Kohlenstoffdioxid, Methanol, Deuterium, Benzol, Wasserstoff, Helium u.a.).
Leider sind dem Autor keine weiteren pvT- Datenangaben bekannt, die qualitativ durch Meßwerte im kritischen Bereich ähnlich der „nist webbook“- Datenbank belegt sind. Es ist deshalb sehr wünschenswert, durch Meßwerte erfaßte pvT- Daten des kritischen Bereichs von weiteren Stoffen zu erhalten, um eine Nachrechnung mit den neuen aus der Theorie kritischer Phänomene nun vorliegenden Berechnungsgleichungen zum Ergebnisvergleich vornehmen zu können.
Aus den zur Theorie kritischer Phänomene durchgeführten Untersuchungen ergeben sich in Bezug auf das Verhalten von Flüssigkeiten wichtige Ergebnisse. Auch Flüssigkeiten besitzen ein pvT- Verhalten. Längst ist das nicht so ausgeprägt wie das von Gasen, da sich das Volumen viel weniger mit Druck und Temperatur ändert. Bei genauer Betrachtung aber, muß die Temperatur- und Druckabhängigkeit des Volumens (z.B. die Abhängigkeit des Sättigungsvolumens von der Temperatur) berücksichtigt werden. Dafür aber gibt es bisher kaum praktikable Theorie- Ansätze auf einer physikalisch begründeten Basis. Alle bisherigen Ansätze zu einer allgemeinen Theorie der Flüssigkeiten gehen letztlich immer vom jeweiligen Molekülaufbau, von den zwischenmolekularen Wechselwirkungen, von molekulartheoretischen Ansätzen der Quantenmechanik und Statistischen Thermodynamik bis hin zur Statistik mit Monte- Carlo- Modellen usw. aus. Die gesuchte Aussage zu einer möglichst allgemeinen Erklärung und mathematischen Fassung der Druck-Volumen- Temperatur- Eigenschaften von Flüssigkeiten wurde so bisher nicht gefunden.
Aus der physikalischen Theorie kritischer Phänomene ergibt sich nun aber eine Zustandsgleichung als eine Näherung speziell für Flüssigkeiten, die keineswegs nur in der kritischen Region, sondern auch für Temperaturen weit unter der kritischen Temperatur gilt. Damit kann nun das mit zunehmendem Druck sich verringernde Volumen einer Flüssigkeit entlang einer Isotherme bzw. anderer Zustandsänderungen berechnet werden- auch wenn diese Effekte klein sind. In der Gemischthermodynamik spielen diese Effekte aber eine weit größere Rolle. Es ist darauf hinzuweisen, daß nun mit Zustandsgleichungen speziell für Flüssigkeiten auch völlig neue Ansätze zur Thermodynamik von Mischungen entstehen. Mit herkömmlichen Zustandsgleichungen für Stoffgemische speziell zur Erfassung der flüssigen Phase sind oft große Schwierigkeiten verbunden, die bis heute nur mit hohem meßtechnischen und empirischen Aufwand für technische Belange gelöst werden müssen.
Die für Flüssigkeiten bestehenden Zustandsfunktionen haben zur Erklärung und Beschreibung des Verhaltens von Flüssigkeiten nur den kritischen Punkt eines Stoffes mit seinen kritischen Phänomenen als Ausgangspunkt, indem die sonst nur in einem engen Bereich um die kritische Temperatur gültigen Gesetze kritischer Phänomene auf Temperaturen weit unterhalb der kritischen Temperatur übertragen werden konnten. Das bedeutet, dass Flüssigkeitseigenschaften allein nur mit den kritischen Daten eines Stoffes und seiner Temperatur festgelegt sind und auch so als Näherung berechnet werden können.
Wegen der nun für Flüssigkeiten und realen Gasen auf Grundlage der Theorie kritischer Phänomene bestehenden pvT- Zustandsfunktionen ergibt sich durch Anwendung des Maxwell- Kriteriums sogar die Möglichkeit, die Sättigungsvolumina v‘ und v“ von Stoffen für Flüssigkeit und Dampf speziell in der kritischen Region in Abhängigkeit von der Temperatur als Näherung zu berechnen. Solch eine Möglichkeit bestand bisher gar nicht. Die Theorie und die Berechnungen dazu sind durchaus kompliziert. Eine kurze zusammenfassende Erklärung ist im Artikel „Die Bestimmung der Sättigungsvolumina von Flüssigkeit und Dampf in der kritischen Region von reinen Stoffen“ dieses Bloggs vom 30.Oktober 2014 gegeben (mit Rechenergebnissen für verschiedene Stoffe im Vergleich zur Datenbank „nist webbook“).
Da auf der Grundlage der zu kritischen Phänomenen durchgeführten Untersuchungen Näherungen zur Bestimmung der Volumina von Flüssigkeit und Dampf in Abhängigkeit von der Temperatur und des Drucks bestehen, können nun auch die sogen. Realgasfaktoren Z = pv/RT eines Stoffes als Temperaturfunktionen im Sättigungszustand als auch allgemein als Funktion des Drucks und der Temperatur berechnet werden. Dazu müssen nur die kritischen Daten eines Stoffes und ein pvT- Datentripel bei niedrigen Dampfdruck und entsprechend niedriger Temperatur bekannt sein (z. B. beim normalen Siedepunkt).
Auf die folgenden Veröffentlichungen des Autors, die die Thermodynamik von Flüssigkeiten und Gasen allgemein und speziell in der kritischen Region von Stoffen betreffen, ist hinzuweisen:
–„Stoffwerte von Flüssigkeiten und Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“, ISBN 978-3-00-027253-0, 2009
– „Die Berechnung von Druck- und Volumendaten reiner Stoffe“, ISBN 3-00-015256-3
– „Neue Berechnungsmöglichkeiten thermophysikalischer Daten für reine Stoffe und Gemische“, ISBN 3-00-018592-5, ISBN 978-3-018592-2.
Die nun einfache Möglichkeit der Berechnung von pvT-Daten in der kritischen Region eines Stoffes
Freitag, März 28th, 2014
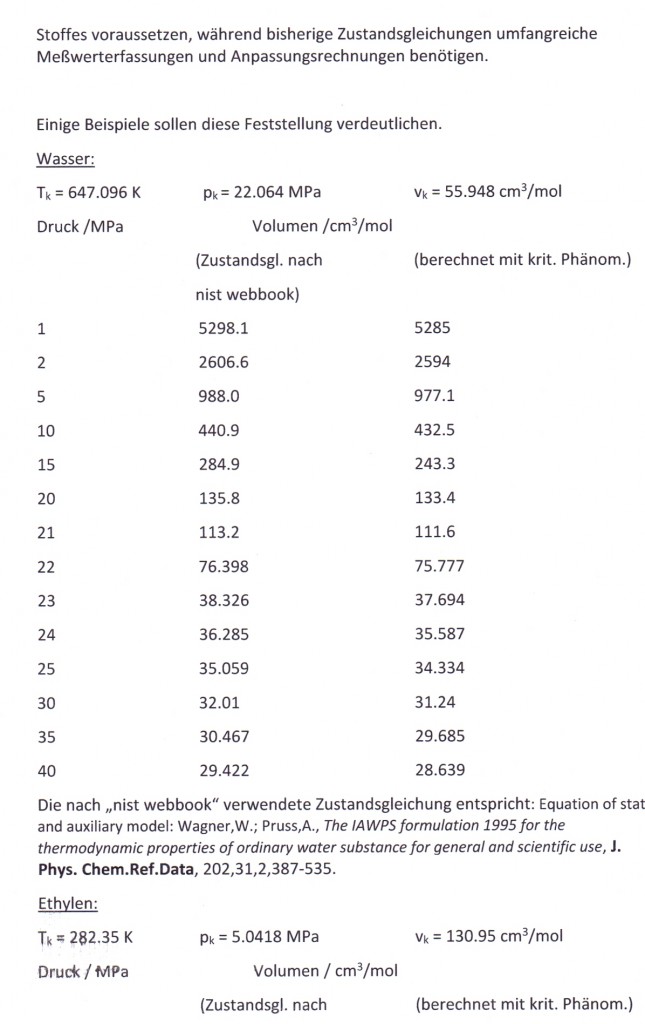


Zur Berechnung von Stoffwerten für Flüssigkeiten und Gase in der kritischen Region von Stoffen
Donnerstag, Januar 23rd, 2014Ganz allgemein ist ja leider festzustellen, daß alle bisherigen in der chemischen Technik und Verfahrenstechnik angewendeten Zustandsgleichungen, selbst die modernsten, nicht in der Lage sind, die realen pvT- Verhältnisse eines Stoffes mit ausreichender Genauigkeit in der kritischen Region darzustellen. Das bestätigen Aussagen zur Genauigkeit in der kritischen Region z. B. auch in der wichtigen und modernen web- site „nist webbook“, die pvT- Werte oft angewendeter Stoffe der chemischen Industrie mit den aktuell besten empirischen Zustandsgleichungen nach Anpassung an Meßwerte angibt (s. auch den Artikel „Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region“ vom 15.4.2013). Auch die Erwartung, daß sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne oder geringe empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Mit nun vorliegenden Untersuchungsergebnissen zum pvT- Verhalten reiner Stoffe in der kritischen Region ist versuchsweise ein Theorie- Ansatz abgeleitet worden, der zu einer Erweiterung von Gesetzmäßigkeiten kritischer Phänomene weit über ihre bisherige Anwendbarkeit begrenzt auf die nahe Umgebung des kritischen Punktes führt. So ergeben sich z. B. Berechnungsgleichungen für die kritische Isotherme und benachbarte Isothermen, die die pvT- Verhältnisse in der Nähe des kritischen Punktes eines Stoffes allein nur bei Kenntnis der kritischen Daten pk, vk, Tk bei guter Annäherung an die Realität wiedergeben. Allerdings ist dieser Ansatz außerhalb des bisherigen Main- Streams. Die von manchen theoretischen Physikern vertretene Ansicht, kritische Exponenten seien analog einer Naturkonstanten unabhängig vom Stoff und etwa konstant, bestätigt sich mit diesem Theorie- Ansatz nur teilweise. Der kritische Exponent β bestätigt sich stoffunabhängig mit ca. 1/3, der Exponent δ allerdings erweist sich als stoffabhängig berechenbar mit den kritischen Daten.
Die van der Waals- Thermodynamik und die vielen auf dieser Grundlage abgeleiteten Zustandsgleichungen gelten ja nicht in der kritischen Region. Hier gelten die Gesetzmäßigkeiten kritischer Phänomene, deren Wirksamkeit nachgewiesen und von der Theorie her erklärt ist- aber doch noch nicht soweit entwickelt ist, dass man für technische Zwecke verlässlich damit rechnen könnte. Veröffentlichte Stoffwerte für Zustände in der kritischen Region können deshalb mit erheblichen Fehlern behaftet sein, wie die Autoren von Stoffwertdaten selbst einschätzen. Die Situation der Bestimmung von Zustandsdaten in der Umgebung des kritischen Punktes eines Stoffes ist bereits in verschiedenen Artikeln dieses Blogs näher dargestellt: „Die Anwendbarkeit kritischer Phänomene zur Berechnung von pvT- Daten“ vom 23.2.2013; „Zur Genauigkeit der Berechnung von pvT-Daten in der kritischen Region“ vom 15.4.2013. Die in Datensammlungen und in der Literatur beschriebenen Berechnungsgrundlagen beziehen sich auf supergenaue Messungen in der kritischen Region und auf jeweils weitgehende empirische Zustandsgleichungen für technisch wichtige Stoffe. Allgemeingültige Lösungen ausreichender Genauigkeit können nicht genannt werden.
Nun ergab es sich nach den o. gen. speziellen Untersuchungen des Verhaltens von Stoffen in der kritischen Region, dass eine Hypothese zur näherungsweisen Erweiterung des Gültigkeitsbereichs kritischer Phänomene sowohl für Zustände um den kritischen Punkt als auch für Zustände weiter entfernt vom kritischen Punkt zu der Realität weitgehend nahekommenden Ergebnissen führt (Angaben zur Theorie und ihre Anwendungen s. z. B. den Artikel „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ vom 1.5. 2009). Nachrechnungen der pv- Daten kritischer Isothermen gut vermessener Stoffe zeigen das, indem die Berechnungsergebnisse entsprechend der neuen zur Theorie kritischer Phänomene abgeleiteten Möglichkeiten mit Ergebnissen von bisher angewendeten Zustandsgleichungen- dokumentiert in „nist webbook“- verglichen werden. Zu betonen ist, dass zur Bestimmung der pv-Werte auf der kritischen Isotherme entsprechend der neuen Berechnungsmöglichkeiten nur die Kenntnis der kritischen Daten pk, vk, Tk notwendig ist, während die von renommierten Autoren angewendeten weitgehend empirischen Zustandsgleichungen umfangreiche Messungen und Anpassungen erfordert haben. Beispiele zum Vergleich der Ergebnisse des neuen Theorie- Ansatzes mit denen nach herkömmlichen weitgehend empirischen Zustandsgleichungen renommierter Autoren auf der Grundlage sehr genauer Messungen und Anpassungen können nach Anforderung (dr.f.tampe@t-online.de) zur Verfügung gestellt werden (für Benzol, Toluol, Ethylen, Kohlenstoffdioxid, Propylen, Helium, Wasserstoff, Methanol…usw.). Auch verwendbare Nachrechnungen für pvT- Daten von Stoffen, zu denen keine Meßwerte außer denen der kritischen Daten in der kritischen Region existieren, sind nun vorstellbar! Das ist durchaus für bisher nicht weiter vermessene Stoffe bei nur der Kenntnis der kritischen Daten zu erwarten (entsprechende Anfragen ebenfalls an die o.gen. Mail- Adresse bei kostenloser Bearbeitung, falls die Ergebnisse nach Absprache zur Auswertung benutzt werden dürfen).
Sehr interessant ist es auch, dass es mit den neuen Möglichkeiten zur Berechnung von pv- Daten auf Isothermen möglich ist, die Sättigungsdaten v‘, v“ von Flüssigkeiten und Dämpfen entsprechend der Temperatur als Näherungen zu bestimmen. Für die v‘-, v“-Volumina von Stoffen kurz unter der kritischen Temperatur eines Stoffes und weiter entfernt von der kritischen Temperatur können so Berechnungsgleichungen abgeleitet werden. Diese Gleichungen geben die Sättigungsvolumina von Flüssigkeiten und Dämpfen als Temperaturfunktion und als Näherung an. Die Genauigkeit der Flüssigkeitsdaten ist dabei oft recht hoch und entsprechend von Meßwerten erheblich besser als die der Dampfdaten. Anfragen zu solchen Nachrechnungen o. gen. Art sind möglich. Es ist darauf hinzuweisen, daß es bisher keine allgemein gültige Möglichkeit gibt, die Sättigungsvolumina von Stoffen als Näherung zu berechnen.
Gedanken zur physikalischen Begründung der heutigen Thermodynamik für Gemische
Sonntag, Dezember 15th, 2013Die zentrale und technisch wichtigste Aufgabe der Thermodynamik von Gemischen ist die Ermöglichung von Phasengleichgewichtsberechnungen.
In technisch vielen Fällen ist ein Flüssigkeitsgemisch mit vorgegebenen Konzentrationen verschiedener Substanzen bei einer vorgegebenen Temperatur der Ausgangspunkt der Berechnungen. Das Ziel der Rechnung ist dann die Bestimmung der dem Siedegleichgewicht entsprechenden Dampfkonzentrationen und des Siededruckes.
Zu dieser zentralen Aufgabe der Gemischthermodynamik existiert eine unglaubliche Vielzahl von Theorien, Methoden und empirischen Vorgehensweisen, die trotz aller praktischen Erfolge leztlich immer noch nicht zu physikalisch begründeten ohne wesentliche Empirie- Anteile auskommenden Berechnungsgleichungen geführt haben.
Die theoretischen Ausgangspunkte von Phasengleichgewichtsberechnungen sind
-Zustandsgleichungen für Gemische und sogen. -Aktivitätskoeffizienten- Modelle.
Grundlage der Rechnung ist immer die Feststellung der partiellen molaren Freien Enthalpie jeder Komponente des Gemisches, denn Gleichgewicht besteht dann, wenn die partiellen Freien Enthalpien der Komponenten in verschiedenen Phasen des Gemisches übereinstimmen.
Alle heute in der Gemischthermodynamik gebräuchlichen Zustandsgleichungen sind letzlich von der physikalisch begründeten van der Waals- Zustandsgleichung, der Virial- Gleichung und Ansätzen der Statistischen Thermodynamik abgeleitet. In vielen technisch wichtigen Fällen sind Weiterentwicklungen der klassischen van der Waals- Gleichung Ausgangspunkt von Phasengleichgewichtsberechnungen geworden. So z. B. die Soave- Redlich-Kwong- Gleichung und die Peng- Robinson- Gleichung, die ausgehend von ihrer für reine Stoffe erklärten Formulierung auch auf Stoffgemische ausgedehnt wurden. Allerdings sind diese Weiterentwicklungen mit erheblichen empirischen Anteilen verbunden, die sich sowohl auf den reinen Stoff als auch auf das Gemisch beziehen. So wird zur besseren Anpassung der Zustandsgleichung an das Realverhalten der Reinstoffe ein sogen. azentrischer Faktor ω eingeführt, der theoretisch fundiert nicht bestimmt werden kann, sondern mit Meßwerten und ausgeprägt empirisch für jeden Stoff zu ermitteln ist. Der empirische Anteil zur Beschreibung der Gemischeigenschaften in heute gebräuchlichen Gemischzustandsgleichungen der Technischen Thermodynamik ist erheblich. Er zeigt sich besonders in dem Teil der Zustandsgleichungen, die den Einfluß der molekularen Wechselwirkungen der Gemischbestandteile darstellen. Das geschieht dann so, daß für jede mögliche Stoffkombination einer Mischung spezielle Parameter der Zustandsgleichung durch Laborversuche festzustellen sind.
Bei der praktischen Anwendung von Gemischzustandsgleichungen ergibt es sich oft, daß das pvT- Verhalten gerade der flüssigen Phase zu ungenau erfaßt ist. Die Berechnung der partiellen Freien Enthalpie zur Bestimmung des Stoffgleichgewichts ist dann ebenfalls viel zu ungenau. Zur Beschreibung flüssiger Gemischphasen werden deswegen heute sogen. Aktivitätskoeffizienten- Modelle angewendet, die es gestatten, sogen. Aktivitäten und damit letzlich die partiellen Freien Enthalpien der Komponenten in der Flüssigkeit mit einer höheren Genauigkeit anzugeben. Ansätze dieser Art sind z.B. die Wilson-, die NRTL- und die UNIQUAC- Gleichung (Wilson, G.M. (1964), J. AM. Chem. Soc. 86 , 127; Renon, H., Prausnitz, J.M. (1968), AIChE J. 21, 116; Abrams, D., Prausnitz, J.M. (1975) AIChE J. 14, 135). Mit solchen Gleichungen gelingt es durchaus, für viele Stoffgemische weitgehend richtige Phasengleichgewichtsberechnungen durchzuführen. Allerdings ist der begriffliche und der empirische Aufwand bei der Anwendung solcher Gleichungen sehr erheblich. So z. B. werden sehr spezielle Daten- wie „relatives van der Waalssches Volumen“, „relative van der Waalssche Oberfläche“ usw. benötigt, die für etliche Reinstoffe empirisch ermittelt in der Literatur vorliegen. Zur Berücksichtigung der Wechselwirkungen zwischen den Molekülen sind weitere spezielle „Wechselwirkungs-Parameter“ definiert, die aus bereits bekannten Phasengleichgewichtsdaten durch Anpassungen erst ermittelt werden müssen. Von einer echten physikalisch begründeten Vorausberechnung des gesuchten Phasengleichgewichts kann also gar nicht die Rede sein, da ja vorher bekannte Gleichgewichtsdaten zur Anpassung andie vorausgesetzten Gleichungen bekannt sein müssen.
Zusammenfassend ist zu sagen, daß der Zwang zur Bereitstellung anwendungsfähiger wenn auch weitgehend empirischer Berechnungsmethoden auf Grund der rasanten chemischen und verfahrenstechnischen Weiterentwicklung der stoffwandelnden Industrie sehr hoch war, so daß die gen. und noch weitere weitgehend empirische Gleichungen zur Phasengleichgewichtsberechnung entstanden sind. Sicherlich ist auch festzustellen, daß die Theoretische Physik bisher nicht inder Lage war, durch Bereitstellung entsprechender Theorie- Vorgaben den Empirie- Anteil wesentlich zu verringern.
Nun ergibt es sich, daß eine ausgehend vom physikalisch begründeten van der Waalsschen Ansatz formulierte Zustandsgleichung für Flüssigkeiten der Variablen p-Druck (MPa), v- Volumen (cm³/mol), T- Temperatur (K)
mit dem Eigenvolumen b (cm³/mol) der Moleküle des Stoffes, einem Parameter K ( der mit dem mit dem Dampfdruck berechenbar ist) und der allgemeinen Gaskonstante R (J/mol K) zu Berechnungsgleichungen für Gemische führt, die es erlauben, Phasengleichgewichte mit einem nur geringen Empirie- Anteil zu bestimmen. Das sogen. Eigenvolumen in obiger Flüssigkeits- Zustandsgleichung erweist sich als berechenbar, wenn nur ein einziger Datenpunkt des jeweiligen Stoffes bekannt ist.
Für Bedingungen niedriger bis mäßiger Drücke führt die Theorie mit obiger Flüssigkeitszustandsgleichung zu relativ einfachen Berechnungsgleichungen des Phasengleichgewichts von Stoffgemischen, die nach ihrer Programmierung per Computer lösbar sind. Man erhält die jeweilige Gemischzustandsgleichung und eine Gleichgewichtsbedingung, die aus der Gleichheit der partiellen Freien Enthalpien der Gemischkomponenten in unterschiedlichen Phasen folgt. Die Formulierung dieser Gleichungen ist nur mit o. gen. Flüssigkeitszustandsgleichung möglich, die das Verhalten von Flüssigkeiten akzeptabel genau beschreibt. So zeigt sich z. B., daß so gar keine „azentrischen Faktoren“ und auch keine sogen. „binären Parameter“, mit denen die Wechselwirkungen zwischen Gemischkomponenten empirisch erfaßt werden müssen, erforderlich sind. Auch die Anwendung der sogen. Aktivitätskoeffizienten- Modelle, die ja weitgehend empirisch formuliert sind, kann so entfallen, da die partiellen Freien Enthalpien bzw. Fugazitäten der Gemischkomponenten ausgehend von einem physikalisch begründeten van der Waals- Ansatz für Gemische dargestellt werden können. Die Theorie dazu und die per Computer programmierbaren Berechnungsgleichungen sind ersichtlich: Tampe, F.:“ Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“, 2009, ISBN 978-3-00-027253-0; „Neue Berechnungsmöglichkeiten thermophysikalischer Daten für reine Stoffe und Gemische“, ISBN 3-00-018582-5, 978-3-018592-2.
Zur Überprüfung der neuen Berechnungsmöglichkeiten wurden exemplarisch binäre und auch ternäre Gemische mit Verhaltensweisen von fast ideal bis hin zu ausgeprägt real untersucht. Es zeigt sich, daß die berechneten Konzentrationen immer einer Näherung im Prozentbereich gegenüber Meßdaten entsprechen. Selbst die Anwendung für extrem reale Gemische- also für Gemische mit Mischungslücke (wie z.B. Wasser- Benzol, Wasser- Butanol, Wasser- Phenol) erweist sich als machbar. Damit ist dann sogar die Berechnung von Löslichkeiten, also z. B. die Berechnung der Löslichkeit von Benzol in Wasser bei guter Übereinstimmung mit Meßwerten möglich.
Die bisher in der technischen Gemisch-Thermodynamik so wichtigen aber weitgehend empirischen Aktivitätskoeffizienten- Modelle sind nun ergänzt durch die Theorie- Schlußfolgerungen für Gemische, die sich aus der o.gen. Flüssigkeitszustandsgleichung ergeben. Aktivitätskoeffizienten können so viel einfacher und ohne spezielle Vorleistungen – wie „relatives van der Waalssches Volumen“, „relative van der Waalssche Oberfläche“ und durch Messungen und Anpassungen zu bestimmende „Wechselwirkungsparameter“ – berechnet werden. Die Theorie dazu und die zur Programmierung erforderlichen Berechnungsgleichungen werden in einer 2014 beabsichtigten Veröffentlichung im Detail dargestellt („Thermodynamik der Flüssigkeiten und realen Gase- alternative Berechnungen mit Gesetzmäßigkeiten kritischer Phänomene“).