
Dieser private Blog dokumentiert ausschließlich Theorie – Ergebnisse der Thermodynamik als Teil der Theoretischen Physik auch zur Fixierung des entsprechenden Urheberrechts. Es erfolgt keine Geschäftstätigkeit, wirtschaftliche Interessen werden nicht verfolgt. Personenbezogene Daten werden nicht erhoben.
In diesem Blog sind neue Theorie- Ergebnisse und ihre praktische Anwendung in der Technischen Thermodynamik dargestellt. Es handelt sich immer um Weiterentwicklungen der klassischen Thermodynamik auf der Grundlage von Zustandsgleichungen und der Anwendung von Gesetzmäßigkeiten kritischer Phänomene zur Berechnung von Stoffdaten speziell der kritischen Region und auch weit unter der kritischen Temperatur. Die Ergebnisse sind zusammengefasst in der Veröffentlichung
„Der erstaunliche Einfluss kritischer Phänomene auf das Zustandsverhalten reiner Stoffe“, ein Forschungsbericht,2019, ISBN 978-3-00-062342-4.
Die Cover- Rückseite dieser Veröffentlichung teilt mit:

Damit bestehen nun Möglichkeiten der Berechnung thermophysikalischer Daten der kritischen Region (als Näherung) und auch weit unter der kritischen Temperatur mit Mitteln der physikalischen Theorie kritischer Phänomene.
Wichtige Artikel dieses Blogs zum Verständnis der Theorie- Grundlagen sind:
– „Die nun mögliche Berechnung von pvT- Daten reiner Stoffe in nahkritischen Zuständen“ – 13.1.2019
– „Die Feststellung weiterer und bisher nicht bekannter kritischer Exponenten und ihre Anwendung“ – 1.1.2019
– „Der erstaunliche Einfluss kritischer Exponenten auf das Verhalten von Flüssigkeiten und Gasen und ihren Sättigungsdaten“ – 3.5.2018
– „Die Soave- Redlich- Keong- Zustandsgleichung völlig neu angewendet für reale Gase, für Flüssigkeiten und zur Berechnung der kritischen Temperatur“ -13.10.2017
– „Die allgemeine Dampfdruckgleichung“ -28.7.2016
An Beispielen wird für etliche Stoffe gezeigt, dass der Dampfdruckverlauf als Temperaturfunktion und die Volumen- bzw. Dichtesättigungswerte in Abhängigkeit von der Temperatur berechnet werden können, wenn nur wenige Messwerte bekannt sind (kritische Daten und die des normalen Siedepunkts). Das z. B. gelingt sogar auch für Metalle und ihre hochsiedenden Verbindungen. Speziell für Metalle u. a. Stoffe wird gezeigt, dass sich die kritische Temperatur, die Dampfdruckfunktion und auch die Sättigungsdaten als Näherungen berechnen lassen, wenn allein nur die pvT- Werte des normalen Siedepunkts bekannt sind.
______________________________________________________________________________________________________________________________________________________________________________
Statt einer der üblichen Zustandsgleichungen für reale Gase kann die folgende einfache Gleichung für den funktionalen Zusammenhang von Druck p/ MPa des Gases, seiner Temperatur T / K und dem spezifischen Volumen v /cm^3/mol angewendet werden:
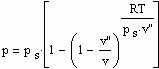 . (1)
. (1)
Dabei ist p.s der Dampfdruck/ MPa und v“ das Sättigungsdampfvolumen / cm^3/mol. R ist die allgemeine Gaskonstante 8.314 J/mol K.
Die obige Gleichung wurde durch eine Erweiterung der physikalischen Theorie kritischer Phänomene auch auf Zustände weit unterhalb der kritischen Temperatur als eine einfache Näherung abgeleitet.
Zwischen dem Volumen v“ des gesättigten Dampfes, der Temperatur T und dem Dampfdruck p.s besteht die folgende Näherungsbeziehung :
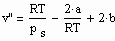 . (2)
. (2)
Die Parameter a, b sind dabei die Konstanten der klassischen van der Waals- Gleichung
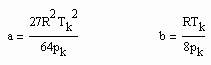 . (3)
. (3)
Damit ist es immer möglich, bei bekanntem Dampfdruck und bekannten kritischen Daten p.k- kritischer Druck/MPa und T.k-kritische Temperatur/ K das Sättigungsdampfvolumen näherungsweise zu berechnen.
Außerdem ist es so auch immer möglich, bei bekanntem Dampfdruck durch Anwendung von Gleichung (1) Zustandsdaten eines realen Gases zu berechnen!
Die komplette Theorie hierzu- auch ein Zusammenhang mit der Theorie der Flüssigkeiten- ergibt sich aus einer Ergänzung der klassischen Thermodynamik durch Schlußfolgerungen aus der physikalischen Theorie kritischer Phänomene und mit einem neuen molekular- theoretischen Ansatz zur Festlegung des Eigenvolumens von Molekülen. Die sich dadurch ergebenden völlig neuen Möglichkeiten der Berechnung
– von p,v,T- Daten realer Gase und Flüssigkeiten ohne Anwendung bisheriger Zustandsgleichungen
-von Sättigungsdaten für Dampf und Flüssigkeit von reinen Stoffen als Temperaturfunktion bis hin zur kritischen Temperatur
– des Dampfdrucks von reinen Stoffen als Temperaturfunktion (ohne Benutzung der sonst üblichen stoffabhängigen Parameter)
– der Verdampfungsenthalpie reiner Stoffe als Temperaturfunktion bis nahe an die kritische Temperatur
– von Freien Enthalpien reiner Stoffe
– sehr genauer Siedevolumina von Flüssigkeiten in Abhängigkeit von der Temperatur
sind in den einzelnen Artikeln dieses Blogs beschrieben.
Notwendige Erläuterung und Zusammenfassung zum Verständnis der wichtigsten Ergebnisse, die dargestellt werden:
Die für Stoffeigenschaften maßgeblichen Wechselwirkungen zwischen den Molekülen und Atomen eines Stoffes haben normalerweise eine Reichweite von nur einigen Molekül- bzw. Atomdurchmessern. Im kritischen Zustand und in seiner Nähe entsteht allerdings ein universelles Verhalten physikalischer Größen wegen des Eintretens sogen. „kritischer Fluktuationen“, die sich wie eine beträchtliche Vergrößerung der Teilchenwechselwirkungen auswirken. Dies hat zur Folge, daß Eigenschaften völlig unterschiedlicher Stoffe sich im nahkritischen Zustand nach analog gleichen Gesetzmäßigkeiten verhalten, so als ob individuelle Stoffeigenschaften verschwinden.
Kritische Phänomene sind z. B. erklärt für
– den Dichtesprung zwischen flüssiger und dampfförmiger Phase
– die Differenz vom Druck zum kritischen Druck bzw. von der Dichte zur kritischen Dichte auf der kritischen Isotherme
– Kompressibilitäten
– Wärmekapazitäten
– magnetische Zustände ( Suszeptibilitäten) bei verschwindendem Feld.
Die Aussagen der klassischen Theorien entsprechend der van der Waals- Gleichung und der darauf aufbauenden empirischen Gleichungen treffen für nahkritische Zustände realer Gase und Flüssigkeiten nicht mehr zu. Für nahkritische Zustände gelten Gesetzmäßigkeiten kritischer Phänomene!
Zum besseren Verständnis der Situation ist folgendes zu erklären: Die theoretische Grundlage zur Beschreibung des Verhaltens realer Gase ist bekanntlich mit der van der Waals- Gleichung und mit der der statistischen Thermodynamik entsprechenden Virialgleichung gegeben. Das ist auch der Ausgangspunkt für viele Weiterentwicklungen- aber dann immer auf weitgehend empirischer Basis.
Die van der Waals- Gleichung beschreibt die Zustände realer Gase und sogar auch von Flüssigkeiten qualitativ richtig, quantitativ aber zur Auslegung technischer Abläufe keineswegs ausreichend. Die Ungenauigkeiten im Zweiphasengebiet und für Daten in der Nähe des kritischen Punktes können groß sein. Vor allem Flüssigkeitszustände werden gar nicht oder nur ungenau erfaßt. Diese Feststellungen betreffen keineswegs nur die van der Waals- Gleichung, sondern auch die in der Technischen Thermodynamik entstandenen „halbempirischen Zustandsgleichungen“ von Soave, Redlich, Kwong und Peng, Robinson u.a., die heute weltweit zur Berechnung von Zustandsdaten angewendet werden.
Die heutigen thermischen Zustandsgleichungen als Grundlage der Berechnung von Stoffdaten für Flüssigkeiten und Gase beruhen alle letzlich auf der physikalisch begründeten van der Waals- Gleichung, der Virialgleichung, auf Ansätzen der statistischen Thermodynamik und vor allem immer wieder auf Parameter- Anpassungen empirischer Berechnungsgleichungen an Meßwerte. Der Aufwand ist hoch. Die empirische Vielfalt ist für Praktiker kaum noch überschaubar. Die unter Physikern manchmal ironisch geäußerte Kritik, daß die sogen. „halbempirischen Zustandsgleichungen“ der Technischen Thermodynamik und Verfahrenstechnik ein selbst empirisch erforderliches Niveau ja eigentlich nur zur Hälfte erfüllen, charakterisiert die Situation.
Die Theoretische Physik muß trotz der unbezweifelbaren verfahrenstechnischen Empirie – Erfolge der letzten Jahrzehnte Richtschnur im Labyrinth der Möglichkeiten bleiben. Die Suche nach physikalisch begründeten neuen Ansätzen mit geringeren empirischen Anteilen sollte gerade auf dem wichtigen Gebiet der Berechnung von Druck p, Volumen v, Temperatur T- Daten aktuell sein und bleiben.
Die für Praxis- Anwendungen erfolgreichen bisherigen Ansätze der Technischen Thermodynamik und Verfahrenstechnik beruhen letzlich immer auf sogen. “ mean- field“- Theorien. Das einzelne Teilchen befindet sich dabei in einem mittleren Feld, das von allen anderen Teilchen verursacht wird. Fluktuationen des einzelnen Teilchens werden vernachlässigt.
In der Nähe des kritischen Punktes gilt diese Näherung nicht mehr, da die stattfindenden Fluktuationen nicht mehr vernachlässigt werden werden dürfen. Die Rechnungen mit den klassischen Theorien führen zu falschen Ergebnissen. Erst mit den nun von der Theoretischen Physik formulierten Gesetzmäßigkeiten kritischer Phänomene können richtige Ergebnisse gewonnen werden.
Eigentlich sollte es naheliegend sein, die Gesetzmäßigkeiten kritischer Phänomene in die Theorie- Ansätze der Technischen Thermodynamik, Physikalischen Chemie und Verfahrenstechnik einzubeziehen. Leider ist das in Bezug auf das Zustandsverhalten von Flüssigkeiten und realen Gasen nicht geschehen, obwohl das- wie sich zeigen wird- möglich ist.
Zum Verständnis der physikalischen Theorie und als kurze Zusammenfassung ist zu sagen: Die Theorie stellt fest, daß sich physikalische Größen f(x) in der Nähe des kritischen Punktes wie
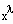
verhalten. Dabei ist x eine Variable, die am kritischen Punkt Null ist. Der Exponent λ wird kritischer Exponent genannt. Er ist mit
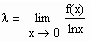
definiert. Bei Existenz des Grenzwertes λ wird- f(x) verhält sich wie
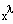
gesagt. Die Definition der kritischen Exponenten umfaßt keineswegs nur die Proportionalität
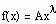 ,
,
sondern auch komplexere Zusammenhänge- wie
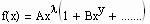 , (A, B,…….Konstanten, y>0).
, (A, B,…….Konstanten, y>0).
Die physikalische Größe f(x) kann der Dichtesprung ρ‘-ρ“ zwischen der flüssigen und dampfförmigen Phase des Stoffes sein, wobei x die Differenz zwischen der jeweiligen Temperatur T und der kritischen Temperatur Tk ist.
Die physikalische Größe f(x) kann auch die Differenz vom Druck p zum kritischen Druck pk auf der kritischen Isotherme sein, wobei x Differenz zwischen der Dichte ρ und der kritischen Dichte ρk auf dieser Isotherme ist.
Für diese beiden kritischen Phänomene werden für nahkritische Zustände im einfachsten Fall die Relationen
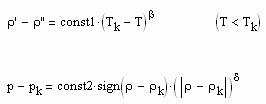
vorausgesetzt. Dabei sind const1 und const2 stoffspezifische Konstanten; sgn ist die Vorzeichenfunktion, die je nach Vorzeichen des Arguments +, – 1 ergibt; die Exponenten β und δ sind kritische Exponenten.
Die Theoretische Physik formuliert eine sogen. Universalitätshypothese: „Die kritischen Exponenten sind fast universell, d. h. für alle thermodynamischen Systeme gleich“ (Nolting: Grundkurs theoretische Physik 6, Statistische Physik, Springer Verlag 2004), (R.B. Griffiths: Phys.Rev.Lett.24,1949(1970)). Diese Hypothese wird unterdessen als bewiesen betrachtet ( Renormierungsgruppentheorie von K. Wilson).
Entsprechend der Universalitätshypothese haben also die kritischen Exponenten β und δ der kritischen Phänomene- Dichtesprung und Druck- bzw. Dichtedifferenz auf der kritischen Isotherme für völlig verschiedene Stoffe die jeweils gleichen Werte. Diese sehr erstaunliche Eigenschaft wird als Folge einer beträchtlichen Vergrößerung der Reichweite von Teilchenwechselwirkungen in der Nähe des kritischen Punktes erklärt.
Der kritische Exponent β wird in der Literatur mit Werten 1/3, 0.34,0.36,0.37 angegeben. Die Variation der Werte ist gering und evtl. mit den Schwierigkeiten der Messung zu erklären.
Der kritische Exponent δ wird mit 4.4 +,- 0.4 angegeben (Nolting, s.o.). Dieser Exponent ist mit einem weitgehend unscharfen Wert von 4.0 bis 4.8 benannt. Die Frage ist, ob für die etwas unterschiedlichen β- Werte und für das große δ- Intervall die Ungenauigkeit der Messung die Ursache ist oder der jeweilige kritische Exponent doch etwas vom Stoff abhängig ist. Selbst Nachfragen bei namhaften theoretischen Physikern konnten diese Frage nicht völlig klären. Teilweise wurde der Hinweis auf feste Werte der kritischen Exponenten entsprechend der Universalitätshypothese gegeben, teilweise wurde eine gewisse Variabilität kritischer Exponenten bei molekular komplizierter aufgebauten Substanzen (bei z. B. C- Doppelbindungen, aromatischen Ringen usw.) nicht ausgeschlossen.
Im Ergebnis der für den Dichtesprung und die kritische Isotherme durchgeführten Untersuchungen ist es möglich, wesentliche Schlußfolgerungen zum Zustandsverhalten realer Gase und von Flüssigkeiten in der Umgebung des kritischen Punktes und für Zustände weit ab von der kritischen Temperatur abzuleiten. Die Erweiterung des Gültigkeitsbereichs von Theorie- Ansätzen kritischer Phänomene nicht nur für Zustände in unmittelbarer Nähe des kritischen Punktes erfolgt als Hypothese unter Einbeziehung mean field- theoretischer Ansätze, die durch die vorliegenden Ergebnisse mit Untersuchungen an konkreten Stoffdaten als berechtigt dargestellt ist.
Für reale Gase niedriger bis hoher Drücke ergibt sich auf dieser Basis ein funktionaler Zusammenhang zwischen dem Druck p und dem molaren Volumen v auf einer Isotherme der Temperatur T entsprechend der Gleichung
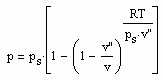 , (I)
, (I)
wobei ps der Dampfdruck, v“ das molare Sättigungsdampfvolumen und R die allgemeine Gaskonstante ist.
Es zeigt sich weiter. daß es mit den hier auf der Grundlage der Theorie kritischer Phänomene gewonnenen Ergebnissen möglich ist, eine allgemeine Beziehung abzuleiten, die die Berechnung des molaren Volumens v“ trocken gesättigten Dampfes bei bekanntem Dampfdruck als Näherung erlaubt:
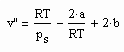 . (II)
. (II)
Dabei sind a und b die Parameter der klassischen van der Waals- Gleichung realer Gase mit a= 27R²Tk²/64pk und b=RTk/8pk, wobei pk der kritische Druck und Tk die kritische Temperatur ist.
Die sinnvolle Anwendbarkeit dieser Gleichung ist für Zustände näherungsweise von niedrigen bis hohen Temperaturen gegeben, nicht aber für nahkritische Verhältnisse (s. oben).
Oftmals liegen Dampfdrücke eines Stoffes als Meßwerte für verschiedene Temperaturen vor, so daß die Abhängigkeit des Dampfdruckes von der Temperatur für sehr viele Stoffe bekannt ist oder mit Näherungen bestimmt werden kann. Für technisch wichtige Stoffe ist so der Dampfdruckverlauf oft bekannt,so daß das Volumen des trocken gesättigten Dampfes in all diesen Fällen mit (II) als Näherung berechnet werden kann.
In Auswertung der zu kritischen Phänomenen durchgeführten Untersuchungen ergab sich weiterhin die folgende Gleichung:
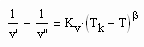 . (III)
. (III)
Dabei ist β ein kritischer Exponent, der hier universell mit β= 1/3 vorausgesetzt ist (s. oben). Kv ist die sogen. Dichtesprungkonstante.
Die obige Gleichung (III), die dem Dichtesprung zwischen Flüssigkeit und Dampf entspricht, ermöglicht die Berechnung des Sättigungsvolumens v‘ der Flüssigkeit bei gegebener Temperatur, wenn v“ bereits mit (II) berechnet werden konnte. Die auf diese Art und Weise berechneten Flüssigkeitsvolumina bzw. Dichten stimmen für die verschiedensten Stoffe erstaunlich gut mit Meßwerten überein.
Für Daten kurz unter der kritischen Temperatur bestehen wegen der am kritischen Punkt sich beträchtlich vergrößernden molekularen Fluktuationen veränderte Bedingungen, die zu anderen sich aus (III) ableitbaren Berechnungsgleichungen führen. Damit sind dann sogar die Sättigungsvolumina v‘ und v“ und auch die Dampfdrücke ps für Temperaturen kurz unter der kritischen Temperatur als Näherungen berechenbar, was mit herkömmlichen thermischen Zustandsgleichungen in Nähe des kritischen Punktes nicht gelingen kann.
Eine in den Variablen p, v, T bestehende thermische Zustandsgleichung werde mit ZG(p,v.T)=0 bezeichnet. Die Zustandsgleichung ZG kann hierbei die van der Waals- Gleichung, die Virialgleichung oder auch eine beliebig andere die Variablen p,v,T enthaltende sinnvolle Zustandsgleichung sein.
Wenn nun für eine bestimmte Temperatur der Dampfdruck gegeben ist, muß

gelten. Außerdem muß das Maxwell- Kriterium
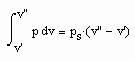 (IV)
(IV)
erfüllt sein.
Es bestehen damit die folgenden zwei Gleichungen als ein Gleichungssystem:
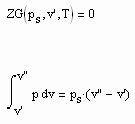 . (V)
. (V)
Da das Gleichungssystem (V) zwei Gleichungen enthält, können zwei Unbekannte bestimmt werden. Bei vorgegebener Temperatur, bekanntem Dampfdruck und den mit den Gleichungen (II) und (III) bekannten Volumina v‘ und v“ können das die in der Zustandsgleichung ZG(p, v, T) =0 enthaltenen unbekannten Parameter der jeweilig vorausgesetzten Zustandsgleichung sein (z.B. der van der Waals-Gleichung, der Redlich- Kwong- Gleichung, der Peng- Robinson- Gleichung usw. ).
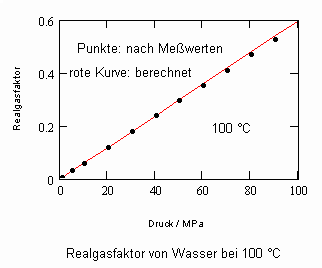
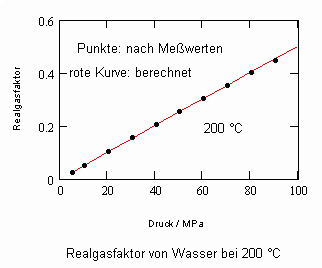
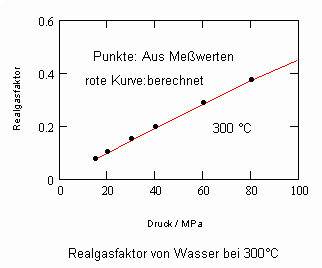
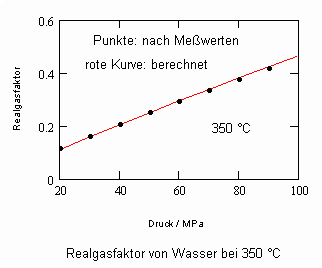
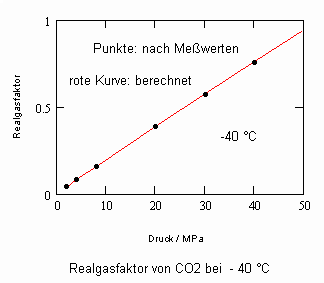
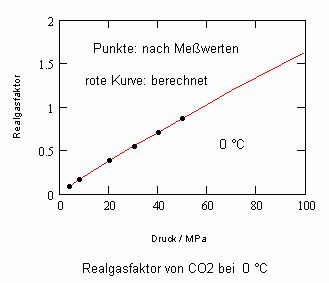
Es zeigt sich, daß man auf diese Art und Weise tatsächlich sinnvolle Ergebnisse erhält. Sowohl für Zustandsgleichungen des van der Waals- Typs als auch für andere können so die Parameter dieser Gleichungen mit (V) berechnet werden. Auf solch einer Grundlage ist dann die Bestimmung von Realgasfaktoren von Flüssigkeiten bei vorgegebener Temperatur vom Dampfdruck bis hin zu hohen Drücken von z. B. 100MPa bei guter Übereinstimmung mit Meßwerten möglich. Die Fehler der Rechnung sind selbst bis zu hohen Drücken gering. Bei Voraussetzung herkömmlicher Zustandsgleichungen sind die Fehler viel größer.
Die Volumina bzw. Dichten realer Gase können für eine bestimmte Temperatur und einen vorgegebenen Druck ohne Benutzung einer der bisher benutzten Zustandsgleichungen mit (I) berechnet werden- die sonst in der Technischen Thermodynamik und Verfahrenstechnik zur Berechnung realer Zustandswerte erforderlichen empirischen Größen- wie z.B. azentrische Faktoren ω sind sind gar nicht mehr erforderlich.
Beispiele für Ergebnisse der Nachrechnungen einzelner technisch interessanter Stoffe sind die Artikel : Tritium, Ozon, Uranhexafluorid, Schwefeldioxid, Stickstoffmonooxid, Aceton, Dioxan, Acetonitril, flüssige Erdgas- und Erdölkomponenten. Für einige flüssige Metalle, für die noch keine herkömmlichen Berechnungsmöglichkeiten existieren, werden die kritischen Temperaturen und die Flüssigkeits- und Sattdampfvolumina eingeschätzt. Auch die Möglichkeit der Formulierung sehr genauer Temperaturfunktionen für das Volumen bzw. für die Dichte von Flüssigkeiten in einem Bereich von der Schmelztemperatur bis nahe unter der kritischen Temperatur wird erläutert.
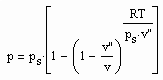 (1)
(1) . (3)
. (3)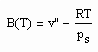 . (4)
. (4)
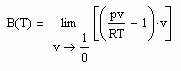 (5)
(5)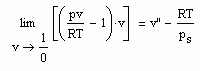
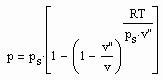 (1)
(1)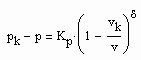 (2)
(2)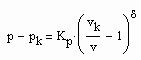 (3)
(3)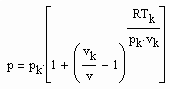 v‹ vk (4)
v‹ vk (4)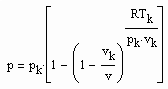 v›vk (5)
v›vk (5)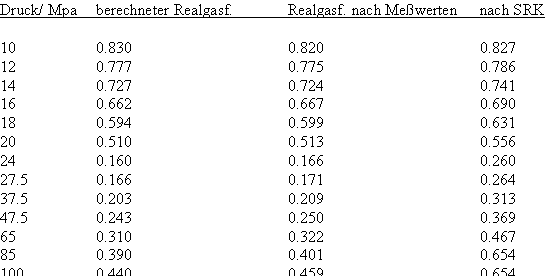

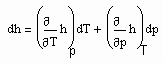 . (7)
. (7) (8)
(8) (9)
(9)



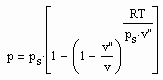 ,
,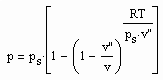
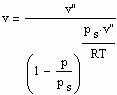
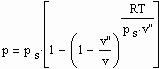 , (1)
, (1)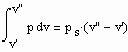 (4)
(4)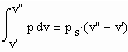 . (5)
. (5)

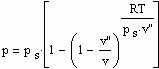 . (1)
. (1)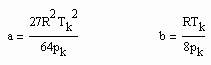 . (3)
. (3)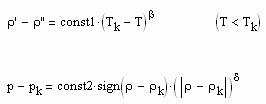
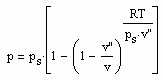 , (I)
, (I)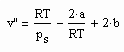 . (II)
. (II)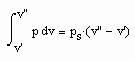 (IV)
(IV)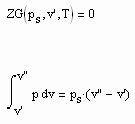 . (V)
. (V)