Archive for the ‘Dichte von Flüssigkeiten und Gasen’ Category
Die nun einfache Möglichkeit der Berechnung von pvT-Daten in der kritischen Region eines Stoffes
Freitag, März 28th, 2014
Zur Berechnung von Stoffwerten für Flüssigkeiten und Gase in der kritischen Region von Stoffen
Donnerstag, Januar 23rd, 2014Ganz allgemein ist ja leider festzustellen, daß alle bisherigen in der chemischen Technik und Verfahrenstechnik angewendeten Zustandsgleichungen, selbst die modernsten, nicht in der Lage sind, die realen pvT- Verhältnisse eines Stoffes mit ausreichender Genauigkeit in der kritischen Region darzustellen. Das bestätigen Aussagen zur Genauigkeit in der kritischen Region z. B. auch in der wichtigen und modernen web- site „nist webbook“, die pvT- Werte oft angewendeter Stoffe der chemischen Industrie mit den aktuell besten empirischen Zustandsgleichungen nach Anpassung an Meßwerte angibt (s. auch den Artikel „Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region“ vom 15.4.2013). Auch die Erwartung, daß sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne oder geringe empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Mit nun vorliegenden Untersuchungsergebnissen zum pvT- Verhalten reiner Stoffe in der kritischen Region ist versuchsweise ein Theorie- Ansatz abgeleitet worden, der zu einer Erweiterung von Gesetzmäßigkeiten kritischer Phänomene weit über ihre bisherige Anwendbarkeit begrenzt auf die nahe Umgebung des kritischen Punktes führt. So ergeben sich z. B. Berechnungsgleichungen für die kritische Isotherme und benachbarte Isothermen, die die pvT- Verhältnisse in der Nähe des kritischen Punktes eines Stoffes allein nur bei Kenntnis der kritischen Daten pk, vk, Tk bei guter Annäherung an die Realität wiedergeben. Allerdings ist dieser Ansatz außerhalb des bisherigen Main- Streams. Die von manchen theoretischen Physikern vertretene Ansicht, kritische Exponenten seien analog einer Naturkonstanten unabhängig vom Stoff und etwa konstant, bestätigt sich mit diesem Theorie- Ansatz nur teilweise. Der kritische Exponent β bestätigt sich stoffunabhängig mit ca. 1/3, der Exponent δ allerdings erweist sich als stoffabhängig berechenbar mit den kritischen Daten.
Die van der Waals- Thermodynamik und die vielen auf dieser Grundlage abgeleiteten Zustandsgleichungen gelten ja nicht in der kritischen Region. Hier gelten die Gesetzmäßigkeiten kritischer Phänomene, deren Wirksamkeit nachgewiesen und von der Theorie her erklärt ist- aber doch noch nicht soweit entwickelt ist, dass man für technische Zwecke verlässlich damit rechnen könnte. Veröffentlichte Stoffwerte für Zustände in der kritischen Region können deshalb mit erheblichen Fehlern behaftet sein, wie die Autoren von Stoffwertdaten selbst einschätzen. Die Situation der Bestimmung von Zustandsdaten in der Umgebung des kritischen Punktes eines Stoffes ist bereits in verschiedenen Artikeln dieses Blogs näher dargestellt: „Die Anwendbarkeit kritischer Phänomene zur Berechnung von pvT- Daten“ vom 23.2.2013; „Zur Genauigkeit der Berechnung von pvT-Daten in der kritischen Region“ vom 15.4.2013. Die in Datensammlungen und in der Literatur beschriebenen Berechnungsgrundlagen beziehen sich auf supergenaue Messungen in der kritischen Region und auf jeweils weitgehende empirische Zustandsgleichungen für technisch wichtige Stoffe. Allgemeingültige Lösungen ausreichender Genauigkeit können nicht genannt werden.
Nun ergab es sich nach den o. gen. speziellen Untersuchungen des Verhaltens von Stoffen in der kritischen Region, dass eine Hypothese zur näherungsweisen Erweiterung des Gültigkeitsbereichs kritischer Phänomene sowohl für Zustände um den kritischen Punkt als auch für Zustände weiter entfernt vom kritischen Punkt zu der Realität weitgehend nahekommenden Ergebnissen führt (Angaben zur Theorie und ihre Anwendungen s. z. B. den Artikel „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ vom 1.5. 2009). Nachrechnungen der pv- Daten kritischer Isothermen gut vermessener Stoffe zeigen das, indem die Berechnungsergebnisse entsprechend der neuen zur Theorie kritischer Phänomene abgeleiteten Möglichkeiten mit Ergebnissen von bisher angewendeten Zustandsgleichungen- dokumentiert in „nist webbook“- verglichen werden. Zu betonen ist, dass zur Bestimmung der pv-Werte auf der kritischen Isotherme entsprechend der neuen Berechnungsmöglichkeiten nur die Kenntnis der kritischen Daten pk, vk, Tk notwendig ist, während die von renommierten Autoren angewendeten weitgehend empirischen Zustandsgleichungen umfangreiche Messungen und Anpassungen erfordert haben. Beispiele zum Vergleich der Ergebnisse des neuen Theorie- Ansatzes mit denen nach herkömmlichen weitgehend empirischen Zustandsgleichungen renommierter Autoren auf der Grundlage sehr genauer Messungen und Anpassungen können nach Anforderung (dr.f.tampe@t-online.de) zur Verfügung gestellt werden (für Benzol, Toluol, Ethylen, Kohlenstoffdioxid, Propylen, Helium, Wasserstoff, Methanol…usw.). Auch verwendbare Nachrechnungen für pvT- Daten von Stoffen, zu denen keine Meßwerte außer denen der kritischen Daten in der kritischen Region existieren, sind nun vorstellbar! Das ist durchaus für bisher nicht weiter vermessene Stoffe bei nur der Kenntnis der kritischen Daten zu erwarten (entsprechende Anfragen ebenfalls an die o.gen. Mail- Adresse bei kostenloser Bearbeitung, falls die Ergebnisse nach Absprache zur Auswertung benutzt werden dürfen).
Sehr interessant ist es auch, dass es mit den neuen Möglichkeiten zur Berechnung von pv- Daten auf Isothermen möglich ist, die Sättigungsdaten v‘, v“ von Flüssigkeiten und Dämpfen entsprechend der Temperatur als Näherungen zu bestimmen. Für die v‘-, v“-Volumina von Stoffen kurz unter der kritischen Temperatur eines Stoffes und weiter entfernt von der kritischen Temperatur können so Berechnungsgleichungen abgeleitet werden. Diese Gleichungen geben die Sättigungsvolumina von Flüssigkeiten und Dämpfen als Temperaturfunktion und als Näherung an. Die Genauigkeit der Flüssigkeitsdaten ist dabei oft recht hoch und entsprechend von Meßwerten erheblich besser als die der Dampfdaten. Anfragen zu solchen Nachrechnungen o. gen. Art sind möglich. Es ist darauf hinzuweisen, daß es bisher keine allgemein gültige Möglichkeit gibt, die Sättigungsvolumina von Stoffen als Näherung zu berechnen.
Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region
Montag, April 15th, 2013Für technisch wichtige Stoffe existieren heute recht genaue Zustandsgleichungen, die die Variablen Druck p, Temperatur T und Volumen v bzw. die Dichte ρ sowohl im Flüssigkeits- als auch im Gaszustand miteinander verbinden. Da es für die in der verfahrenstechnisch – großtechnischen Praxis bestehenden Anforderungen auf eine hohe Genauigkeit ankommt, reichen Berechnungsgleichungen auf Modellvorstellungen der Theoretischen Physik (auf der Basis der van der Waals- Gleichung und ihren vielen sogen. halbempirischen Weiterentwicklungen, der Virialgleichung usw. bis hin zur sogen. molekularen Thermodynamik) nicht aus. Deshalb müssen immer noch Zustandsgleichungen mit ausgeprägt empirischen und stoffspezifischen Anteilen verwendet werden, um die erforderliche Genauigkeit zu ermöglichen. Der Aufwand ist hoch. Er setzt sehr genaue und umfangreiche pvT- Messungen des jeweiligen Stoffes voraus, um die erforderlichen Anpassungen der experimentell ermittelten Zustandsdaten an Parameter vorausgesetzter Zustandsgleichungen zu ermöglichen. Die Erfolge dieser Vorgehensweise mit weitgehend empirischen und „halbempirischen“ Zustandsgleichungen sind offensichtlich.
Selbst für den die menschliche Existenz begründenden Stoff „Wasser“ sind solch weitgehend empirische Zusammenhänge auf der Grundlage sehr genauer pvT- Messungen entwickelt worden (entsprechend der sogen. IAPWS formulation- „International Association for the Properties of Water and Steam“), keineswegs aber auf der alleinigen Grundlage eines nur physikalisch begründeten Modells. Auch für die wichtigen Stoffe der Erdöl- und Erdgasgewinnung und Verarbeitung- wie z.B. Methan, Ethan……bis Benzol, Toluol usw.- existieren Zustandsgleichungen dieser Art.
Meßwerte vieler Substanzen sind heute in Datenbanken dokumentiert, die einen schnellen Zugriff (allerdings oft gebührenpflichtig) über das Internet gestatten (s. z.B. die umfangreiche Stoffdatensammlung „dechema.de/detherm“). Die Bereitstellung von Stoffdaten geht unterdessen so weit, für eine Vielzahl technisch wichtiger Stoffe komplette pvT-Datensätze und auch kalorische Daten anzugeben (s. „nist webbook“), die nach Vorgabe von Druck und Temperatur entsprechend der jeweiligen Dichte bzw. des Volumens mit einer weitgehend an Meßwerte angepaßten Zustandsgleichung ermittelt wurden- und das sowohl für die flüssige Phase und auch für die Gasphase und überkritische Zustände. Die Fehler dabei sind durchaus gering und liegen oft nur im Prozentbereich oder sogar darunter. Sie sind so geeignet für verfahrenstechnische Auslegungen großtechnischer Prozesse mit solchen Stoffen.
Dies alles trifft zu nur für pvT- Zustände weiter entfernt von den kritischen Daten. Soll bei Vorgabe von Druck und Temperatur in einem nahkritischen Bereich die Dichte bzw. das Volumen eines Stoffes mit einer solchen Zustandsgleichung bestimmt werden (dokumentiert z.B. in „nist webbook“) ist das zwar möglich- die Fehler aber werden dann oft als „höher“ im Vergleich zu den Fehlern angegeben, die in Zuständen weiter entfernt von den kritischen Daten festgestellt sind. So heißt es dann z.B. bei nist webbook für Ammoniak: „The uncertainties of the equation of state are o.2% in density….., except in the critical region“.
Und so etwa lauten ähnliche Feststellungen für auch ander Stoffe:
– „Uncertainties will be higher near the critical point“- nist webbook für H2S
– „In the critical region the uncertainties are higher for all properties, except vapor pressure“- nist webbook für SO2.
Die Liste von Stoffen mit der Aussage „except in the critical region“ zu den in der Literatur angegebenen Zustandsgleichungen kann fortgesetzt werden, z. B. mit solchen grundlegenden und strukturell einfachen Stoffen wie Pentan, Propylen, Methan u.a. So ist also die Feststellung gerechtfertigt, dass die Ungenauigkeiten bisheriger veröffentlichter Zustandsgleichungen speziell in der kritischen Region selbst nach den durchgeführten sehr genauen pvT-Messungen und Anpassungen immer noch recht hoch sind. Der Aufwand ist hoch in Relation zum Ergebnis.
Die Hoffnung, dass sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Nun hat es sich aus theoretischen Erwägungen zur Physik kritischer Phänomene ergeben, einen anderen als bisherige Ansätze zur Auswertung dieser Phänomene zu verfolgen.
Das bisherige Theorie- Ergebnis ist, dass man bei Kenntnis nur der kritischen Daten eines Stoffes weitgehend zutreffende Näherungsaussagen zum pvT- Verlauf der kritischen Isotherme bzw. von nahkritischen Isothermen erhalten kann- ohne zusätzliche Meßwerte. Für Stoffe also, zu denen keine weiteren Messungen außer denen der kritischen Daten vorliegen, können dann zumindest Näherungen des Isothermen -Verlaufs in der kritischen Region abgeleitet werden. Da das für sehr, sehr viele Stoffe zutrifft, ist es also durchaus möglich, die Daten der kritischen Isotherme und auch pv-Daten etwas unterhalb und oberhalb der kritischen Temperatur als Näherung zu berechnen. Nähere Ausführungen zur Theorie und zu Beispielrechnungen sind im Artikel vom 1.7.12 in www.dr-tampe.de u.a. enthalten.
Bisher war es nicht möglich, die Sättigungsvolumina der siedenden Flüssigkeit und des Sattdampfes für Temperaturen kurz unter der kritischen Temperatur vorauszuberechnen. Mit den neuen Theorie- Ergebnissen zu kritischen Phänomenen erweist sich das unterdessen als möglich. Die berechneten Volumina sind Näherungen, die durchaus weitgehend mit Meßwerten übereinstimmen (s. Artikel“ Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur“ in www.dr-tampe.de .)
Zur Berechnung nahkritischer Stoffdaten von Flüssigkeiten und Gasen
Sonntag, Juli 1st, 2012Aus der physikalischen Theorie kritischer Phänomene kann für reale Gase die Zustandsfunktion
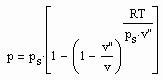(1)
für Zustände entfernt vom kritischen Punkt bzw. für kleine bis mäßige Drücke abgeleitet werden (p- Druck/ MPa, ps- Dampfdruck/ MPa, T- Temperatur / K, v- molares Volumen / cm³/mol, v“- molares Sattdampfvolumen / cm³/mol ). Die Funktion (1) ist als grobe Näherung anwendbar. Sie ist anwendbar auch für hohe Temperaturen, sogar bis über die kritische Temperatur hinaus. Ihre Anwendbarkeit für Zustände nahe des kritischen Punktes ( einige Kelvin unterhalb und oberhalb der kritischen Temperatur Tk und für Drücke in der Nähe des kritischen Druckes pk ) ist nicht zu erwarten, da hier besondere und andere Bedingungen gelten, die sich aus Gesetzmäßigkeiten kritischer Phänomene im Unterschied zur bisherigen van der Waals- Thermodynamik ergeben.
Auf der kritischen Isotherme können entsprechend der Gesetzmäßigkeiten kritischer Phänomene nahe des kritischen Druckes die Relationen
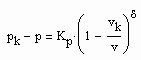(2)
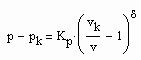(3)
vorausgesetzt werden. Dabei ist Kp ein Proportionalitätsfaktor und δ der entsprechende kritische Exponent. (2) gilt für p ‹ pk , (3) gilt für p › pk.
Für p,v – Zustände nahe pk, vk ist (2), (3) zwingend mit einem in der Theorie kritischer Phänomene erklärten kritischen Exponenten zu rechnen. Der kritische Exponent δ ist resultierend aus Messungen in der Größenordnung von 4.0 bis 4.8 festgestellt worden (s. z. B. Nolting, W.: Statistische Physik, Springer Verlag 2004). Es gibt Physiker, die kritische Exponenten im Sinne absoluter Naturkonstanten unabhängig vom Stoff interpretieren und andere, die eine Stoffabhängigkeit in Grenzen zugestehen. Setzt man die weitgehende Stoffunabhängigkeit voraus, verbleibt der Proportionalitätsfaktor Kp als Unbekannte. Es besteht die Frage, wie ist der Proportionalitätsfaktor Kp zu bestimmen, um Zustände auf der kritischen Isotherme berechnen zu können?
Sinnvoll ist es, die Frage allgemeiner zu stellen. Nämlich: Wie können nahkritische Zustandsdaten mit ausreichender Genauigkeit nicht nur für Zustände auf der kritischen Isotherme, sondern auch für Temperaturen kurz unter- und oberhalb der kritischen Temperatur bestimmt werden? Bisherige physikalisch begründete als auch die sogen. halbempirischen Zustandsgleichungen u.a. reichen nicht aus. Auch die von der bisherigen Theoretischen Physik erklärten Ansätze, die die rechnerische Bestimmung des Proportionalitätsfaktors Kp ohne Meßwerte kaum erlauben, reichen nicht aus. Für technisch wichtige Stoffe ist deshalb die Physikalische Chemie und Verfahrenstechnik auf empirische stoffspezifische Lösungen bei einem hohen meßtechnischen Aufwand angewiesen (vielparametrige empirische Zustandsgleichungen pro Stoff bei Voraussetzung hochgenauer Stoffwerte) ( s. z. B. die Stoffdaten für Erdgaskomponenten, für Kohlenstoffdioxid CO2, für Wasser usw. mit weitgehend empirischen Zustandsgleichungen von Wagner und Span, Universität Bochum, s. E.W. Lemmon u. R. Span: Multiparameter Equations of State for Pur Fluids and Mixtures. Chapter 12, in A.R.H. Goodwin, J.V. Sengers und C.Peters(Ed.): Applied Thermodynamics of Fluids. International Union of Pure and Applied Chemistry, Royal Society of Chemistry, Thomas Graham House,Cambridge, UK 2010)).
Bisherige Feststellungen und Schätzungen kritischer Exponenten für dreidimensionale physikalische Systeme mit einem Ordnungsparameter in der entsprechenden Universalitätsklasse wurden z. B. in Auswerung des Issing – Modells mit dem kritischen Exponenten β = 0.326 + – 0.002 und δ = 4.80+- 0.02 vorausgesetzt (s. z. B. J.V. Senger: Thermodynic Behavior of Fluids near the critical Points, Ann. Rev. Phys.Chem. 1986,37).
Vorliegende Ergebnisse zu Gesetzmäßigkeiten kritischer Phänomene bestätigen zwar die Existenz des kritischen Exponenten β in der Größenordnung von 1/3, nicht aber die Gültigkeit eines allgemeinen Exponenten δ etwa bei 4.8. Das in der Theoretischen Physik gen. Werteintervall δ = 4.0 bis 4.8 trifft zu und ist nach den vorliegenden Untersuchungen durchaus noch zu klein.
Die nachfolgenden Feststellungen weisen darauf hin, daß es möglich ist, einen physikalisch begründeten und empiriefreien Ansatz zur Nachrechnung nahkritischer Daten ohne zusätzlichen Meßaufwand zu finden.
Bestimmt man für die kritische Isotherme vergleichsweise für verschiedene Stoffe den Exponenten RTk/pk vk in (1), ist festzustellen: Es gibt Stoffe, deren Exponent RTk/pk vk in (1) in dem für den kritischen Exponenten δ erklärten Bereich zwischen 4.0 bis 4.8 liegt. Für Wasser z. B. ergibt sich 4.36, für Ammoniak NH3 4.12. Für solche Stoffe ist die weitgehende Gültigkeit der Funktion (1) auch im nahkritischen Bereich zu erwarten. Die kritische Isotherme sollte in diesen Fällen entsprechend (1) mit
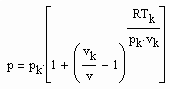v‹ vk (4)
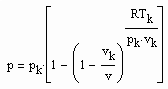v›vk (5)
erfaßt werden können.
Ob das tatsächlich so ist, zeigt die Nachrechnung mit Daten gut vermessener Stoffe wie z. B. für Wasser.
Wasser: (Tk= 647.15 K, pk= 22.055 MPa, vk= 55.9503 cm³/mol)
Bei einer Temperatur 648.15 K (375 °C, also 1°C über der kritischen Temperatur) und einem hypothetischen Dampfdruck von 22.286 MPa ergeben sich mit den o. gen. Funktionen (4), (5) im Vergleich mit aus Meßwerten berechneten Realgasfaktoren die folgenden Werte (außerdem sind die Werte angegeben, die sich mit einer der oft angewendeten Ingenieurgleichungen, der Soave- Redlich- Kwong- Gleichung berechnen lassen).
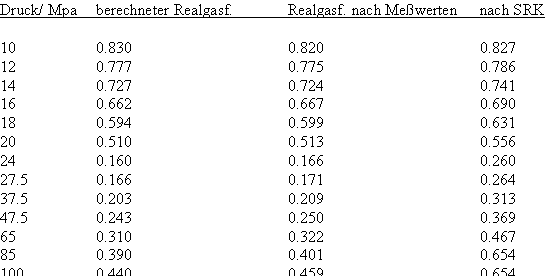
(Meßwerte L. Haar, J.S. Gallagher, G.S. Kell: NBS/NRC Wasserdampftafeln, Springer 1988)
Ein weiteres für die kritische Isotherme vermessenes und veröffentlichtes Beispiel ist
Schwefelhexafluorid SF6: (Tk= 318.7232 K, pk= 3.755 MPa, vk= 196.576 cm³/mol)
Bei einer Temperatur genau auf der kritischen Isotherme ergeben sich mit den o.gen. Funktionen (4), (5) im Vergleich mit aus Meßwerten berechneten Realgasfaktoren die folgenden Werte:
Die gen. Beispiele u.a. zeigen die Anwendbarkeit der Funktionen (4), (5) für kritische Verhältnisse.
Für Stoffe allerdings, deren Exponent RTk/ pk vk nicht in das von der physikalischen Theorie erklärte Wertebereich von ca. 4.0 bis 4.8 für kritische Exponenten fällt, bestehen andere Bedingungen. Allerdings ergibt sich auch für solche Stoffe die Möglichkeit, nahkritische Stoffdaten rechnerisch zu bestimmen. Es ist dazu nur die Kenntnis der kritischen Daten und die vorausgesetzte Temperatur ohne weitere Meßwerte erforderlich.
Die so feststellbare Zustandsfunktion p = p(T,v) gestattet dann auch die Berechnung kalorischer Größen- wie auch der wichtigen Freien Enthalpie für nahkritische Zustände.
Die vorliegenden Theorie – Ergebnisse sollen veröffentlicht werden.
Die sich aus der Theorie kritischer Phänomene ergebenden Weiterentwicklungen ermöglichen es, allgemeine Aussagen zum pvT- Verhalten von Flüssigkeiten abzuleiten. Es ergibt sich eine Zustandsfunktion speziell für Flüssigkeitenvon niedrigen Temperaturen bis hin zu Temperaturen nahe der kritischen Temperatur. Damit kann bei vorgegebener Temperatur und vorgegebenem Druck das molare Volumen einer Flüssigkeit als Näherung selbst bis zu hohen Drücken von einigen 10 MPa und höher berechnet werden, wenn nur die kritischen und die Sättigungsdaten des jeweiligen Stoffes bekannt sind. Die Berechnung der Realgasfaktoren von Flüssigkeiten bis zu hohen Drücken ist somit bei guter Übereinstimmung mit Meßwerten möglich.
Für Flüssigkeitszustände bei Temperaturen niedriger bis mäßiger Dampfdrücke, d.h. weiter entfernt vom kritischen Punkt des jeweiligen Stoffes, ist mit den Mitteln der van der Waals- Thermodynamik die Zustandsfunktion
(6)
ableitbar (b- Eigenvolumen der Moleküle des Stoffes/ cm³/mol, K-stoffspezifische Konstante mit der Dimension eines Druckes, die sich aus dem Dampfdruck ergibt) (s. Tampe,F.: Stoffwerte von Flüssigkeiten und Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene, 2009, ISBN 978-3-00-027253-0).Auch diese Funktion ermöglicht die Berechnung der Flüssigkeitsvolumina als Näherung für Drücke vom Dampfdruck bis weit darüber hinaus- z.B. für Wasser sogar bis 100 MPa. Mit dieser Funktion (6) und der aus der physikalischen Theorie kritischer Phänomene ableitbaren Zustandsfunktion für Flüssigkeiten nahe kritischer Werte ist die Berechnung von Flüssigkeitsdaten als Näherung in ihrem gesamten Existenzbereich von niedrigen bis zu hohen Temperaturen, vom Dampfdruck bis zu hohen Drücken möglich.
Die in der Technischen Thermodynamik , Physikalischen Chemie und Verfahrenstechnik bestehenden Ansätze, Stoffeigenschaften mit den Mitteln der bisherigen van der Waals- Thermodynamik, der Statistischen Thermodynamik mit Mitteln von Potential- Ansätzen der Quantenmechanik bzw. der sogen. molekularen Modellierung zu bestimmen, erweisen sich oft als kompliziert und empiriebelastet. Als viel einfacher gestalten sich die aus Gesetzmäßigkeiten kritischer Phänomene ableitbaren Berechnungsgleichungen, die nicht einmal Anpassungsrechnungen an vorausgesetzte empirische Parameter verlangen.
Weitere Beispiele zu Rechenergebnissen im Vergleich zu Meßwerten können die Anwendbarkeit der gewonnenen Theorie – Ergebnisse, die Näherungen der entsprechenden Stoffwerte erlauben, verdeutlichen: s. Anlage.
Oftmals sind Meßwerte des nahkritischen Sättigungszustandes von Stoffen unbekannt. Die Berechnung solcher Daten für Flüssigkeits- und Dampfvolumina bzw. für Dampfdrücke in der Nähe der kritischen Temperatur ist mit den gegenwärtig verfügbaren Berechnungsgleichungen (van der Waals- Gleichung, sogen. halbempirische Gleichungen nach Soave, Redlich, Kwong und Peng, Robinson u. a., Gleichungen der Statistischen Thermodynamik usw.) in vielen Fällen nicht möglich bzw. zu ungenau.
In Auswertung von Gesetzmäßigkeiten kritischer Phänomene ergibt sich nun die Möglichkeit, nahkritische Sättigungsvolumina bzw. die nahkritischen Dichten von Stoffen für Flüssigkeit und Dampf im Sättigungszustand in Abhängigkeit von der Temperatur zu berechnen. Die Berechnungsgleichungen dafür liegen vor. Die Ergebnisse sind Näherungen, die für den Flüssigkeitszustand sogar besser sind als für den Sattdampf (s. auch Artikel „Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur“ vom 22.2.2011 in www.dr-tampe.de )
Auf Folgendes ist hinzuweisen: Wenn die Zustandsfunktion p= p(v,T) eines Stoffes sowohl sowohl für den Flüssigkeits- als auch für den Gaszustand bekannt ist, muß es möglich sein, kalorische Daten dieses Stoffes zu berechnen. Zur Berechnung z.B. der für technische Belange wichtigen Enthalpie gilt
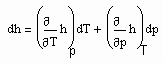. (7)
Da
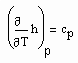(8)
die spezifische Wärmekapazität ist, die gemessen werden kann, und für
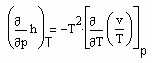(9)
gilt, ist damit die Enthalpie eines Stoffes sowohl für den Flüssigkeitszustand als auch den Gaszustand berechenbar. Dies bedeutet weiter, daß so die Enthalpie eines Stoffes entlang der Dampfdruckkurve sowohl für die Flüssigkeit als auch für den Sattdampf als Näherung berechnet werden kann.
Anlage: Berechnungsbeispiele
Die Berechnung von Flüssigkeitsdaten
Mittwoch, November 2nd, 2011Speziell für Flüssigkeiten kann physikalisch begründet die Zustandsgleichung
abgeleitet werden. Dabei ist T die absolute Temperatur / K , p der Druck über der Flüssigkeit / MPa, ps der Dampfdruck der Flüssigkeit/ Mpa, v das molare Volumen/ cm³/mol, b das molekulare Eigenvolumen/ cm³/mol und K eine dimensionslose Konstante. Diese Gleichung gilt für Flüssigkeiten entsprechend Temperaturen niedriger Dampfdrücke bis zu Temperaturen höherer Dampfdrücke, nicht aber in der Nähe der kritischen Temperatur.
Das Moleküleigenvolumen b ist als die Summe der einzelnen Volumina, die die Moleküle des Stoffes durch ihre atomare Strucktur im Raum aufspannen, erklärt. Das Eigenvolumen erweist sich über weite Temperaturbereiche (von niedrigen bis zu hohen Temperaturen, nicht aber in der Nähe der kritischen Temperatur) als konstant. Es kann mit Stoffdaten, die für niedrige Dampfdrücke gelten, berechnet werden- z. B. mit den (p,v,T)- Daten des oft bekannten normalen Siedepunkts, ebenso ist auch die obige Größe K festgelegt. Zu den Einzelheiten der Theorie s. “ Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0).
Für etliche technisch wichtige Stoffe sind die sogen. Realgasfaktoren Z = pv/RT sowohl für die Gas- als auch für die Flüssigphase entlang einer Isotherme von niedrigen bis zu hohen Drücken erfaßt. Diese Daten sind aus Stoffdatenbanken oder aus Stoffwertsammlungen (s. z. B. W. Blanke: „Thermophysikalische Stoffgrößen“, Springer Verlag) zu entnehmen. Es handelt sich um versuchstechnisch ermittelte Werte. Die Nachrechnung dieser Werte mit den heute in physilalischer Chemie und Verfahrenstechnik bekannten Zustandsgleichungen führt oft zu Ergebnissen, die mit den Meßwerten nicht übereinstimmen. Vor allem bei Flüssigkeiten ist das so, da es für Flüssigkeiten bisher keine allgemein anwendbare und physikalisch begründete Zustandsgleichung gab. Die o.gen. Flüssigkeits- Zustandsgleichung ermöglicht es allerdings nun, Flüssigkeitsvolumina bei vorgegenem Druck und gegebener Temperatur bei weitgehender Übereinstimmung mit Meßwerten zu berechnen bzw. die Realgasfaktoren zu bestimmen.
Die Tatsache, daß die bisher auch für Flüssigkeiten angewendeten Zustandsgleichungen von van der Waals und ihre Modifikationen zu oft ungenauen Ergebnissen führen, ist als Theorie- Tatsache durchaus bekannt, da es eine physikalisch ausgearbeitete Theorie der Flüssigkeiten bisher nicht gibt. Interessant ist deshalb das Ergebnis einer Umfrage zu diesem Thema. Es wurde die Frage gestellt, ob es unterdessen Möglichkeiten zur Berechnung von Flüssigkeits- Realgasfaktoren bis zu hohen Drücken von 50 bis 100 MPa mit geringen Fehlern gegenüber Ergebnissen aus Meßwerten gibt. Es wurde gefragt: Ist es überwiegend in der Praxis noch so, daß für Flüssigkeiten nur eigens durchgeführte pvT- Messungen zum Ziel führen? Fachlich fundierte Antworten bestätigten, daß es bisher noch keine physikalisch begründeten allgemein gültigen Ergebnisse aus einer Theorie der Flüssigkeiten gibt, die es ermöglichen würde, Realgasfaktoren für Flüssigkeiten vom Dampfdruck bis zu hohen Drücken auf einer Isotherme mit ausreichender Übereinstimmung mit Meßwerten zu berechnen.
Aber es gab auch ganz andere Antworten. Z. B. die, man solle dazu unter „google scholar“ nachsehen. Oder gar keine Stellungnahmen. Oder die: Es gibt Berechnungsmöglichkeiten.
Die o. gen. speziell für Flüssigkeiten bestehende Gleichung wurde mit einer Vielzahl von Stoffbeispielen immer mit dem Ergebnis weitgehender Übereinstimmung mit Meßwerten überprüft. Einige Beispiele dazu sind im Artikel “ Erdgas- flüssig “ vom 4.3. 2010 bereits genannt. Vor allem ist auf den Artikel „Die Zustandsdaten von Flüssigkeiten- berechnet von niedrigen bis hohen Drücken“ vom 6.2.2010 in diesem Zusammenhang hinzuweisen.
Die nachfolgenden Diagramme für Realgasfaktoren solch wichtiger Stoffe wie Wasser und Kohlenstoffdioxid bei verschiedenen Temperaturen können die gute Übereinstimmung zwischen Rechnung mit obiger Gleichung und Meßwerten zeigen.
Wasser- flüssig:
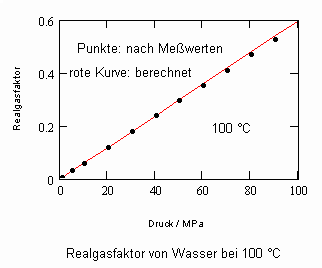
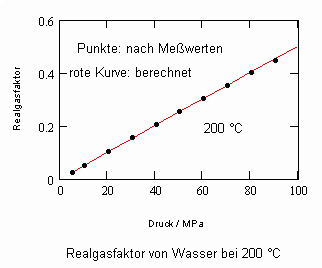
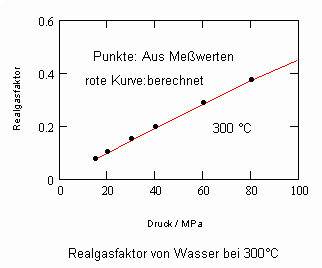
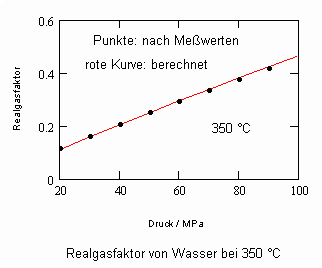
Kohlenstoffdioxid CO2- flüssig:
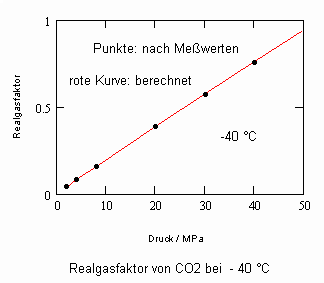
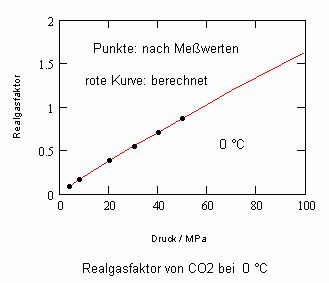
Die gute Übereinstimmung zwischen Rechnung und den Werten aus Versuchsdaten ist für die wichtigen Beispiele Wasser und Kohlenstoffdioxid ersichtlich. Ein weitgehend linearer Verlauf des Realgasfaktors Z in Abhängigkeit vom Druck auf einer Isotherme ist ersichtlich.
Für viele Stoffe, auch technisch wichtige Stoffe, ist die Druckabhängigkeit von Flüssigkeitsdaten noch gar nicht bekannt. Nur für absolut wichtige Stoffe- wie z. B. Wasser, Kohlenstoffdioxid, Methan, Ethylen, Propan, Butan, Stickstoff, Ammoniak, Sauerstoff- sind Realgasfaktoren druckabhängig bei verschiedenen Temperaturen als allgemein zugängige Daten (ohne evtl. vorhandene Angaben aus gebührenpflichtigen Datenbanken) auf der Grundlage von Meßwerten erfaßt. Mit der o. gen. Flüssigkeitszustandsgleichung besteht nun die Möglichkeit, den Verlauf des Realgasfaktors einer Flüssigkeit zumindest als Näherung zu erfassen, wenn allein nur die pvT- Daten des normalen Siedepunkts des Stoffes vorliegen (oder auch nur das molare Volumen bei einer Temperatur niedrigen Dampfdrucks).
Die eingangs gen. Flüssigkeitszustandsgleichung wird gelöst, indem bei vorgegebenem Druck und vorgegebener Temperatur das jeweilige molare Volumen gesucht wird. Bei der überwiegenden Zahl der Lösungen liegt jeweils nur ein Volumenwert vor, so daß als Realgasfaktor immer nur ein Wert Z = pv/RT entsteht. Interessanterweise existieren aber auch p,T- Zustände von Flüssigkeiten, für die sich nach obiger Gleichung nicht nur eine Lösung für das molare Volumen ergibt, sondern sogar zwei! Das bedeutet, daß es in solchen Flüssigkeitszuständen zumindest mathematisch auch zwei Realgasfaktor- Werte gibt.
An den Beispielen Wasser und Kohlenstoffdioxid soll das näher erläutert werden.
Für Wasser bei 300 °C und einem Druck von 10 MPa ergibt sich rechnerisch ein Realgasfaktor Z1 = 0.049, der mit dem entsprechenden Wert 0.051 auf der Grundlage von Meßwerten gut übereinstimmt. Außerdem ergibt sich aber auch noch ein zweiter Wert Z2 = 0.186. Bei einem Druck von 15 MPa ebenfalls bei 300 °C ist Z1 = 0.073 und Z2 = 0.32 feststellbar. Der Wert Z1 stimmt gut mit dem auf der Basis von Meßwerten sich ergebenden Realgasfaktor 0.078 überein. Nur im Bereich der Temperatur von 300 °C und Drücken von ca. 10 bis 15 MPa ist eine zweite Lösung Z2 überhaupt feststellbar. Alle anderen untersuchten Wasser- Zustände von 100 bis 350 °C und Drücken bis 100 MPa haben immer nur eine Z- Lösung, die mit den Werten nach Messungen gut übereinstimmen.
Die Frage ist: Was bedeutet die Lösung Z2, die nur in einem eng begrenzten Druck- und Temperaturbereich erklärt ist?
Auch für Kohlenstoffdioxid sind ähnlich wie bei Wasser in einem eng begrenzten p,T- Bereich zwei Lösungen der angewendeten Flüssigkeitszustandsgleichung feststellbar, so daß für bestimmte p,T- Zustände jeweils zwei Realgasfaktoren genannt werden müssen. Für Kohlenstoffdioxid z. B. bei -40 °C und einem Druck von 2 MPa ist Z1 = 0.04 und Z2 = 0.4 feststellbar. Der Wert Z1 stimmt mit dem mit Meßwerten ermittelten Wert o.o405 gut überein. Bei einer Temperatur von 0 °C und einem Druck von 4 MPa ergibt sich Z1 = 0.0845. Dies stimmt gut dem Wert 0.08305 überein,der sich nach Meßwerten ergibt. Für einen zweiten Wert gilt Z2 = 0.172. Ähnlich wie im Fall Wasser ist die zweite Lösung in einem nur engen Zustandsbereich erklärt (ca. von -40°C bis 0 °C und relativ niedrigen Drücken).
Auch hier ist die Frage zu stellen, was bedeutet die zweite Lösung Z2, die nur in einem engem Druck- und Temperaturbereich erklärt ist?
Es gibt nur zwei Erklärungsmöglichkeiten. Prinzipiell besteht die Möglichkeit, daß die Lösung Z2 ohne eine physikalische Bedeutung allein nur durch die mathematische Strucktur der o.gen. Flüssigkeitszustandsgleichung zu Stande kommt. Sicherlich muß man diesen Fall präferieren. Die andere Möglichkeit würde folgendes bedeuten: Für einen bestimmten vorgegebenen Druck und eine bestimmte vorgegebene Temperatur einer Flüssigkeit können zwei molare Volumenwerte existieren, so daß in diesem Fall zwei Realgasfaktoren feststellbar sind. Dies würde allerdings weiter bedeuten, daß in einem engen p,T- Zustandsbereich einer Flüssigkeit zwei Modifikationen des Stoffes mit zwei unterschiedlichen Dichten existieren können – ρ1 = M/v1, ρ2 = M/v2 (M- relative Molmasse g/mol). Sollte solch eine Möglichkeit tatsächlich bestehen? Es ist sehr fraglich. Andererseits ist die evtl. Existenz der beiden Flüssigkeitsmodifikationen in einem jeweils nur sehr engen p,T- Bereich erklärt, zu dem in Bezug auf eine zweite Modifikation wegen ihrer Unwahrscheinlichkeit bisher gar keine Untersuchungen vorliegen können.
Was sollte getan werden?
Experimente z.B. mit Wasser bei ca. 300 °C und Drücken um 10 bis 15 MPa könnten darüber aufklären, ob es eine zweite Flüssigkeitsmodifikation entsprechend der obigen Flüssigkeits- Zustandsgleichung überhaupt gibt. Der Autor dieses Artikels ist dazu nicht in der Lage. Gibt es fachlich Interessierte, die die Gültigkeit und Aussagekraft der gen. Flüssigkeits- Zustandsgleichung mit den dazu notwendigen Technik- Einrichtungen überprüfen könnten und wollen? Allerdings besteht das Risiko, nur bestätigt zu bekommen, daß es nur die eine Flüssigkeitsmodifikation gibt. Falls allerdings bestätigt werden sollte, daß es in einem engen p,T- Bereich eine zweite Flüssigkeitsmodifikation geben kann, ist der wissenschaftliche Gewinn erheblich.
Die Zustandsdaten von Flüssigkeiten- berechnet von niedrigen bis hohen Drücken
Samstag, Februar 6th, 2010In atomistischer Betrachtungsweise ist ein Festkörper bzw. ein Kristall mit einer starren Anordnung seiner Gitterbausteine aufgebaut. Die Gitterbau-steine können Schwingungen gegeneinander ausführen. Das Verhalten und das energetische Niveau des Festkörpers werden wesentlich von den Schwingungen der Gitterbausteine bestimmt. Die von den Gitterbausteinen des Festkörpers ausgeführten Schwingungen entsprechen den Wechselwirkungen im Gitter.
Fehlt die zwischenmolekulare Wechselwirkung vollständig, liegt ein ideales Gas vor. Beim Beginn zwischenmolekularer Wechselwirkungen der Moleküle bzw. der Atome des Stoffes liegt ein reales Gas vor.
Beim Festkörper bzw. Kristall tritt beim Übergang zur Flüssigkeit eine Fluktuation der Molekülpositionen auf.
Der Unterschied zwischen einer Flüssigkeit und einem realen Gas äußert sich im Verhältnis von kinetischer Energie und potientieller Energie der Moleküle bzw. Atome des Gases. Die kinetische Energie des Gases ist größer als die potientielle und es existiert eine freie Weglänge , die viel größer als die Ausdehnung der Molekülwechselwirkungen ist.
Flüssigkeiten entsprechen also Zuständen zwischen realen Gasen und Festkörpern.
Eine wichtige Grundlage zur Beschreibung des Verhaltens realer Gase ist bekanntlich die van der Waals- Gleichung. Sie ist der Ausgangspunkt für viele Weiterentwicklungen- aber dann immer auf weitgehend empirischer Basis.
Die klassische van der Waals- Gleichung beschreibt die Zustände realer Gase und sogar auch von Flüssigkeiten qualitativ richtig, quantitativ aber zur Auslegung technischer Abläufe keineswegs ausreichend. Die Ungenauigkeiten im Zweiphasengebiet und für Daten in der Nähe des kritischen Punktes können groß sein. Vor allem Flüssigkeitszustände werden sehr ungenau oder gar nicht erfaßt. Diese Feststellungen betreffen keineswegs nur die van der Waals- Gleichung, sondern auch die in der Technischen Thermodynamik entstandenen sogen. „halbempirischen Zustandsgleichungen“ von Soave, Redlich, Kwong und Peng, Robinson u. a. , die heute weltweit zur Berechnung von Zustandsdaten angewendet werden.
So ist es bis heute nicht gelungen, die physikalische Theorie so zu entwickeln, daß die Volumina bzw. Dichten von Stoffen temperaturabhängig entlang der Dampfdruckkurve mit genügender Genauigkeit von der Schmelztemperatur bis zur kritischen Temperatur berechnet werden können. Oftmals besteht auch die Situation, daß mit den gegebenen Gleichungen zwar das Dampf- und Gasverhalten gut erfaßt werden kann, nicht aber die Flüssigkeitswerte.
Die heutigen thermischen Zustandsgleichungen als Grundlage der Berechnung von Stoffdaten für Flüssigkeiten und Gase beruhen alle letztlich auf der physikalisch begründeten van der Waals- Gleichung, der Virialgleichung, auf Ansätzen der statistischen Thermodynamik und vor allem auf Parameter- Anpassungen der Berechnungsgleichungen an Meßwerte. Die empirische Vielfalt ist für einen Praktiker kaum noch überschaubar.
Die unter Physikern manchmal ironisch geäußerte Kritik, daß die sogen. „halbempirischen Zustandsgleichungen“ der Verfahrenstechnik und Technischen Thermodynamik ein selbst empirisch erforderliches Niveau ja eigentlich nur zur Hälfte erfüllen, charakterisiert die Situation.
Die Theoretische Physik muß trotz der unbezweifelbaren verfahrenstechnischen Empirie – Erfolge Richtschnur im Labyrinth der Möglichkeiten bleiben. Die Suche nach physikalisch begründeten neuen Ansätzen mit geringeren empirischen Anteilen sollte gerade auf dem Gebiet der Berechnung von p,v,T- Daten aktuell sein und bleiben.
Wenig untersucht ist die Möglichkeit, Gesetzmäßigkeiten der physikalischen Theorie kritischer Phänomene auszuwerten und sogar evtl. auf die Berechnung thermophysikalischer Daten anzuwenden.
Kritische Phänomene sind für nahkritische Zustände eines Stoffes erklärt als spezielle und weitgehend allgemeingültige Abhängigkeiten zwischen Druck, Temperatur, Volumen, Wärmekapazität usw. Wichtig ist evtl. der Schritt, den Versuch zu unternehmen, Gesetzmäßigkeiten kritischer Phänomene auch auf Zustände weiter ab vom kritischen Zustand als Näherung anzuwenden.
Beispielsweise erweist es sich alternativ auf solch einer Grundlage als durchaus möglich, die Siededichten von Stoffen mit hoher Genauigkeit zu berechnen, ohne auch nur eine der heute üblichen Zustandsgleichungen zu benutzen. Es muß dazu jeweils nur der kritische Druck, die kritische Temperatur und ein weiterer Datenpunkt mit Angaben für Temperatur, Druck und Dichte für einen Zustand niedrigen Dampfdrucks (z. B. beim normalen Siedepunkt) vorliegen (Parameter wie ω als azentrischer Faktor und alle anderen mit vielen empirischen Voraussetzungen erklärten Parameter sind gar nicht notwendig!).
Selbst Realgasfaktoren für reale Gase und sogar Flüssigkeiten unter hohem Druck können so als Näherung berechnet werden- ohne die Verwendung einer der bisher üblichen Zustandsgleichungen.
Auch Taudichten eines Stoffes lassen sich auf der Grundlage von Gleichungen, die sich aus Gesetzmäßigkeiten kritischer Phänomene ergeben, näherungsweise berechnen.
Der alternative Ansatz über die Theorie kritischer Phänomene in Verbindung mit herkömmlichen molekulartheoretischen Vorstellungen- wie sie z.B. zur Herleitung der van der Waals- Gleichung notwendig waren- führt zu neuen Berechnungsmöglichkeiten für Zustände realer Gase und für Flüssigkeiten. Der Zugang zu einer allgemeinen Theorie der Flüssigkeiten wird dadurch evtl. nicht auf der Grundlage bisheriger Ansätze und Vorstellungen auf rein molekulartheoretischer Grundlage und der statistischen Thermodynamik, sondern in Verbindung dieser Grundlagen mit der physikalischen Theorie kritischer Phänomene ermöglicht. Allerdings ist zu sagen, daß zu all diesen alternativen Möglichkeiten der Übertragung von Gesetzmäßigkeiten kritischer Phänomene auf die Berechnung von Zuständen weiter entfernt von den kritischen Daten die physikalische Begründung letzlich noch fehlt. Hier besteht Forschungsbedarf! Klar aber ist, daß sich mit den abgeleiteten neuen Gleichungen als Näherungen richtig rechnen läßt. Die Überprüfung dieser Möglichkeiten erfolgte durch die Nachrechnung an gut vermessenen Stoffbeispielen.
Im Ergebnis der durchgeführten Untersuchungen zeigt sich speziell für Flüssigkeiten, die unter ihrem Dampfdruck bis zu hohen Drücken stehen können, daß das (p,v,T)- Zustandsverhalten von Flüssigkeiten richtig erfaßt werden kann, wenn Gesetzmäßigkeiten kritischer Phänomene auf Zustände weitab vom kritischen Punkt übertragen werden (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“- ISBN 978-3-00-027253-0). Es ist auf solch einer Grundlage möglich, sowohl das Siedevolumen v‘ der Flüssigkeit als auch das Sattdampfvolumen v“ eines Stoffes als Näherung zu berechnen, wobei vor allem die Flüssigkeitswerte erstaunlich gut mit Meßwerten übereinstimmen. Dies alles erweist sich als möglich ohne Voraussetzung einer speziellen Zustandsgleichung bzw. einer empirischen Zustandsgleichung mit Parametern, die durch Anpassung an Meßwerte erst bestimmt werden müssen.
Die Rechenprogramme hierzu liegen vor.
Bei formaler Voraussetzung der klassischen van der Waals- Gleichung als physikalisch begründete Zustandsgleichung
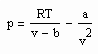
(p- Druck/ MPa, T- Temperatur / K, v- spezifisches Volumen / cm³/mol, b- Eigenvolumen / cm³/mol, a- Parameter / MPa (cm³/mol)²) sind bei vorgegebener Temperatur, bekanntem Dampfdruck ps und den berechneten sich aus der erweiterten Theorie kritischer Phänomene ergebenden Flüssigkeits- und Dampfvolumina v‘ und v“ die Parameter a und b unbekannt bei Voraussetzung dieser Parameter als mit der Temperatur veränderliche Größen. Es bestehen also zwei Unbekannte- nämlich a und b.
Die Verbindung zwischen Flüssigkeits- und Dampfdaten wird durch das Maxwell- Kriterium
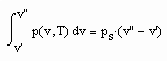
hergestellt.
Es bestehen also zwei Gleichungen für die beiden unbekannten Parameter a, b, die somit bestimmt werden bei Vorgabe der Volumina v‘ und v“, die sich allein mit Gesetzmäßigkeiten kritischer Phänomene berechnen lassen. Die so berechneten Parameter a, b entsprechen keineswegs den mit der klassischen van der Waals- Gleichung benutzten a, b- Werten. Die Unterschiede sind erheblich.
Werden nun die berechneten Parameter a,b der vorausgesetzten o. gen. Zustandsgleichung zu Grunde gelegt, können bei vorgebener Temperatur und vorgegebenem Druck die entsprechenden Flüssigkeitsvolumina bzw. Dichten und die entsprechenden Realgasfaktoren Z = pv/RT selbst bis zu nahkritischen Zuständen berechnet werden. Die Ergebnisse erweisen sich für Volumina durchaus immer in der Nähe der Meßwerte bzw. der aus Meßwerten berechneten Realgasfaktoren. Die dafür erforderlichen Berechnungen liegen programmiert vor. Alle bisher in diesem Blog für Flüssigkeiten gen. Berechnungsergebnisse wurden auf die geschilderte Art und Weise gewonnen. Die Theorie dazu ist aus der Broschüre „Stoffwerte von Flüssigkeiten und realen Gasen -berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0) zu ersehen.
Voraussetzung zur Nutzung der aufgezeigten Berechnungsmöglichkeiten ist allerdings das Vorliegen der kritischen Daten des jeweiligen Stoffes. Aber gerade diese Angaben sind nicht immer bekannt. Trotzdem besteht zumindest für Zustände bei Temperaturen , die niedrigen Dampfdrücken entsprechen, auch bei unbekannten kritischen Daten die Möglichkeit, zu Ergebnissen zu gelangen. Für solche Zustände nämlich vereinfachen sich die Berechnungsgleichungen für die Parameter a und b. Die Daten des kritischen Punktes sind nun nicht mehr zur Berechnung des Parameters a und des Eigenvolumens b erforderlich.
So können also immer z.B. für den normalen Siedepunkt eines Stoffes die Parameter a und b mit diesen vereinfachten Gleichungen berechnet werden, da sich die Daten des normalen Siedepunkts leicht aus den für viele Stoffe vorliegenden Stoffdatensammlungen ergeben oder auch oft einfach durch Messung bestimmbar sind.
Das Eigenvolumen b, das so für Zustände bei Temperaturen niedrigen Dampfdrucks bestimmt wird, hat die äußerst interessante Eigenschaft, über weite Temperaturbereiche fast konstant zu sein. Es variiert nur gering in einem Temperaturbereich des jeweiligen Stoffes bei niedrigen bis mäßigen Dampfdrücken von einigen MPa. Die Theorie und nähere Einzelheiten hierzu sind in der Broschüre „Die Berechnung von Druck- und Volumendaten reiner Stoffe“ (ISBN 3-00-015256-3) dargelegt.
Diese spezielle Eigenschaft der fast bestehenden Konstanz des Eigenvolumens bei Temperaturen niedrigen Dampfdrucks kann zur Berechnung von von (p,v,T)- Daten eines Stoffes sinnvoll ausgenutzt werden. Man braucht nur das Eigenvolumen für einen bekannten Datenpunkt des Dampfdrucks pso, des Siedevolumens v’o und der Temperatur To (z.B. für den normalen Siedepunkt) zu berechnen, um bei anderen Temperaturen, vorgegebenen Druck und dem schon berechneten Eigenvolumen das entsprechende Volumen bzw. die Dichte der Flüssigkeit mit einer speziellen Flüssigkeitszustandsgleichung bestimmen zu können.
Mit dieser speziell für Flüssigkeiten geltenden Zustandsgleichung ist es tatsächlich möglich, bei gegebenem Dampfdruck das Siedevolumen v‘ bzw. bei vorgegebenem Druck (über dem Dampfdruck) das entsprechende Flüssigkeitsvolumen zu berechnen. Damit kann dann auch der Realgasfaktor Z = pv/RT der Flüssigkeit bis zu hohen Drücken bestimmt werden.
Berechnungsbeispiele zur Anwendung der hier für Flüssigkeiten aufgezeigten Möglichkeiten werden in nachfolgenden Artikeln angegeben.