Am kritischen Punkt eines Stoffes können thermodynamische Funktionen ganz besondere und unerwartete Eigenschaften aufweisen. Im kritischen Punkt divergiert die spezifische Wärmekapazität, die Kompressibilität, die magnetische Suszeptibilität und die sogenannte Korrelationslänge. Andere Größen, wie die Dichte bzw. das Volumen eines Stoffes bleiben endlich.
Um diese Erscheinungen einheitlich zu beschreiben, wurden sogenannte kritische Exponenten ψ eingeführt, die sich mit der jeweiligen temperaturabhängigen thermodynamischen Funktion f(T) entsprechend
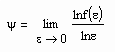
ergeben. Dabei ist ε die sogenannte reduzierte Temperatur
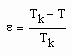 ,
,
die bei Annäherung an die kritische Temperatur Tk gegen Null geht.
Äußerst interessant ist nun die Feststellung der Theoretischen Physik, daß die kritischen Exponenten für bestimmte thermodynamische Funktionen unabhängig vom Stoff und der jeweiligen Daten des kritischen Punktes gleiche bzw. etwa gleiche Werte haben sollen.
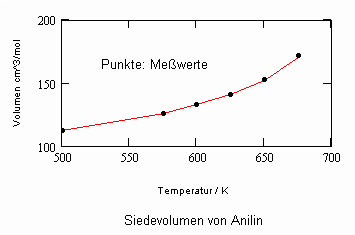
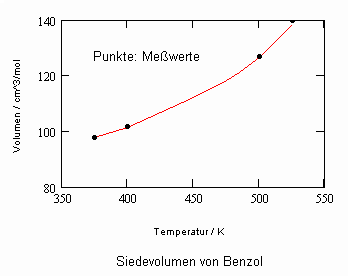
Für die Dichtedifferenz ρ′—ρ″ zwischen siedender Flüssigkeit und dem entsprechendem Sattdampf wird ein kritischer Exponent mit dem Wert β=1/3 festgestellt. Mit der o.gen. Definitionsgleichung des kritischen Exponenten und seinem für die Dichtedifferenz ρ′-ρ″ festgestellten Wert ist es möglich, Schlußfolgerungen zum Verlauf der gen. Dichtedifferenz eines Stoffes in Abhängigkeit von der Temperatur als Reihenentwicklung abzuleiten. Damit ergeben sich sehr genaue Berechnungsgleichungen der Siededichte eines Stoffes als Temperaturfunktion von der Tripelpunktemperatur bis fast hin zur kritischen Temperatur. Nur wenige Meßwerte der Siededichte müssen dazu zur Anpassung von Parametern der Berechnungsgleichung bekannt sein. Einige Beispiele können das belegen.
Anilin:
Benzol:
Wasser:
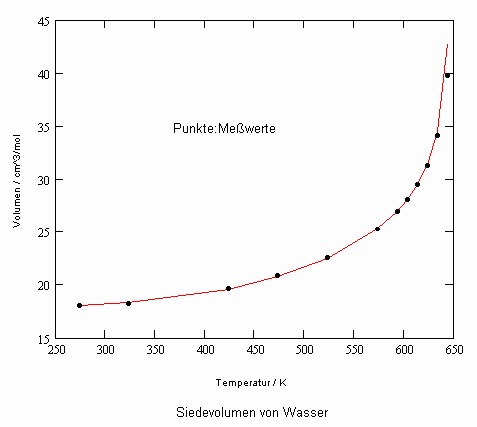
Ergänzend wird außerdem noch der relative Fehler des berechneten molaren Volumens für Wasser angegeben.
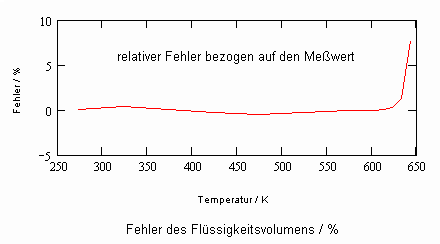
Zur Berechnung der o.gen. Daten wurden neben den kritischen Werten (kritischer Druck, kritische Temperatur) außerdem noch die Tripelpunktwerte für Temperatur und Volumen, die Werte des normalen Siedepuntes und noch ein weiterer Datenpunkt mit Temperatur und Volumen vorausgesetzt. Die Fehler liegen- wie ersichtlich- sehr niedrig!