Falls die Aufgabe besteht, die Sättigungsvolumina v‘ und v“ bzw. die Dichten ρ‘ und ρ“ eines Stoffes für Temperaturen kurz unter der kritischen Temperatur Tk dieses Stoffes rechnerisch zu bestimmen, können sich bei Verwendung bisher üblicher Zustandsgleichungen erhebliche Abweichungen gegenüber Meßwerten ergeben.
Wenn die kritischen Daten mit dem kritischen Druck und der kritischen Temperatur bekannt sind, wird selbstverständlich eine der üblichen verfahrenstechnischen Zustandsgleichungen angewendet (evtl. die van der Waals- Gleichung, die Soave- Redlich- Kwong- Gleichung, die Peng- Robinson – Gleichung oder andere). Ist auch der Dampfdruck ps bekannt, sind die Sättigungsvolumina entsprechend der jeweiligen Zustandsgleichung mit
ps = p(v‘,T), ps = p(v“,T)
berechenbar. Ganz abgesehen davon, daß sich je nach der vorausgesetzten Zustandsgleichung unterschiedliche Ergebnisse herausstellen, ist das Hauptproblem aber folgendes: Die mit herkömmlichen Zustandsgleichungen berechneten Daten für Zustände kurz unter der kritischen Temperatur stimmen oftmals gar nicht mit Meßwerten überein. Die Fehler sind groß.
Für Wasser z. B. (als einer der für die menschliche Existenz wichtigsten Stoffe) sind die sich mit der Soave- Redlich- Kwong – Gleichung berechenbaren Sättigungsvolumina für nahkritische Zustände den Meßwerten in den nachfolgenden beiden Diagrammen gegenübergestellt. Die großen Differenzen zwischen berechneten Daten und Meßwerten sind ersichtlich. Das etwa ist so nicht nur für Wasser!
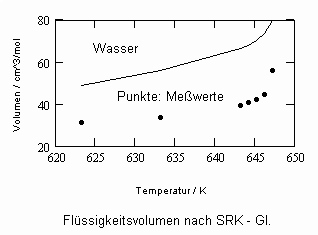
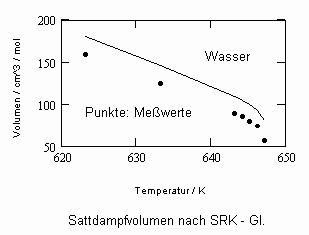
Der Rechnung wurde die Soave- Redlich- Kwong- Gleichung, die eine der weltweit meist angewendeten empirischen Zustandsgleichungen ist mit
p = RT/v-b -a/v(v+b)
und
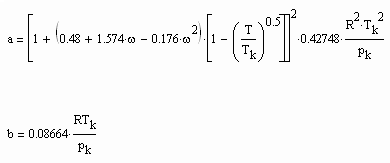
zu Grunde gelegt (dabei ist ω ein empirisch für jeden Stoff festzulegender Faktor).
Bei der Wertung der Situation ist es wichtig, nicht nur die Tatsache von teilweise großen Ungenauigkeiten herkömmlicher Zustandsgleichungen zu berücksichtigen, sondern auch vor allem die Erkenntnis, daß Zustandsgleichungen – basierend auf der klassischen van der Waals-Gleichung und ihren empirischen Weiterentwicklungen- in der unmittelbaren Nähe der kritischen Temperatur prinzipiell gar nicht mehr gültig sein können. Der Grund sind die in der Nähe des kritischen Punktes auftretenden kritischen Phänomene. Die Reichweite der zwischenmolekularen Wechselwirkungen vergrößert sich und divergiert sogar, die molekulare Individualität scheint sich zu verlieren, es gelten für unterschiedliche Stoffe sich etwa angleichende Verhaltensweisen- eben die Gesetzmäßigkeiten kritischer Phänomene. Aber das sind nicht mehr die Bedingungen und Voraussetzungen der klassischen van der Waals- Thermodynamik. Es stellt sich heraus, daß herkömmliche Zustandsgleichungen in der Umgebung des kritischen Punktes prinzipiell nicht anwendbar sind (s. z. B. hierzu F. Schwabl: „Statistische Mechanik“, Spinger- Verlag 2004).
Die aus der physikalischen Theorie kritischer Phänomene abgeleitete Beziehung
![]() ,
,
die ohne Verwendung einer herkömmlichen Zustandsgleichung besteht, gilt auch in unmittelbarer Nähe zum kritischen Punkt (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“- ISBN 978-3-00-027253-0).
Kurz unter der kritischen Temperatur gilt auch etwa
![]()
(s. z. B. Schwabl, „Statistische Mechanik“, Springer Verlag 2004). Damit kann nun sowohl das Flüssigkeitsvolumen v‘ als auch das Dampf- Sättigungsvolumen v“ als grobe Näherung für Zustände kurz unter der kritischen Temperatur berechnet werden. Es ergibt sich für das Flüssigkeitsvolumen v‘ für einige K kurz unter der kritischen Temperatur die quadratische Gleichung
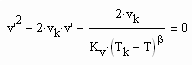 ,
,
die durchaus Meßwerten nahe kommende Werte für das Flüssigkeitsvolumen v‘ und für das Dampfvolumen v“ liefert.
Die oben vorausgesetzte Symmetrie der Differenz des Flüssigkeits- bzw. Dampfvolumens zum kritischen Volumen gilt i. a. jeweils nur einige K unter der kritischen Temperatur. Für von der kritischen Temperatur weiter entfernte Zustände sind bessere Lösungen erforderlich, die tatsächlich existieren. Programme zur rechnerischen Bestimmung der Sättigungsdaten für Flüssigkeits- und Dampfzustände verschiedenster Stoffe sind auf der Grundlage kritischer Phänomene abgeleitet. Die so berechneten Daten erweisen sich als den Meßwerten viel besser entsprechend als Ergebnisse mit herkömmlichen Zustandsgleichungen.
Für einige Stoffe soll das exemplarisch belegt werden.
Für Wasser sind in den beiden nachfolgenden Diagrammen die so berechneten Flüssigkeits- und Dampfvolumina für den Sättigungszustand bei verschiedenen Temperaturen angegeben.
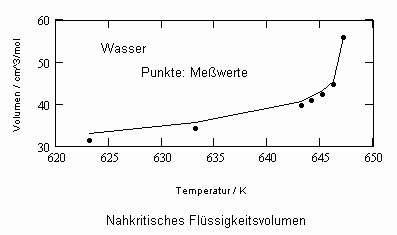
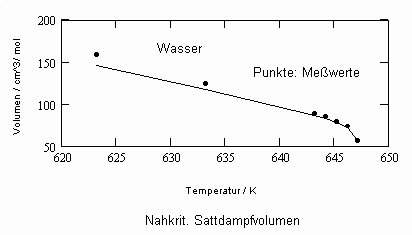
Die für Wasser sehr deutlichen positiven Unterschiede der Berechnungsergebnisse, die mit diesen Diagrammen im Vergleich zu den eingangs angegebenen Diagrammen entsprechend der Soave- Redlich- Kwong- Gleichung festzustellen sind, sind erheblich.
Für zwei weitere Beispiele – Ethylen und Kohlenstoffdioxid- seien Ergebnisse der v‘, v“- Nachrechnung im Vergleich mit Meßwerten genannt.
Berechnete nahkritische Flüssigkeits- und Sättigungsdampfdaten für Ethylen sind in den beiden nachfolgenden Diagrammen im Vergleich mit Meßwerten dargestellt:
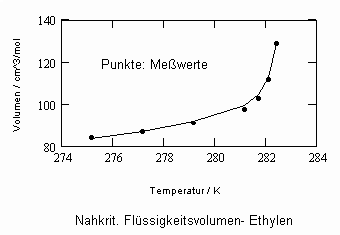
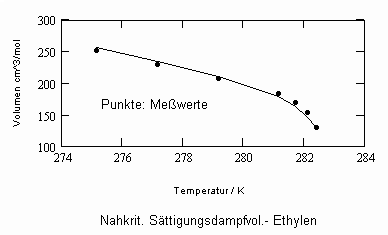
Die für Kohlenstoffdioxid CO2 berechneten v‘, v“- Werte sind im Vergleich mit Meßwerten und mit nach der Soave- Redlich-Kwong- Gleichung berechneten Werten in den beiden folgenden Diagrammen dargestellt:
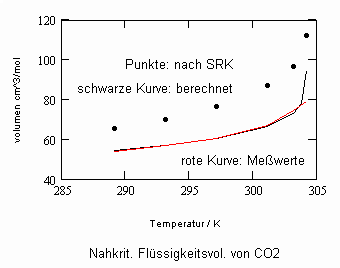
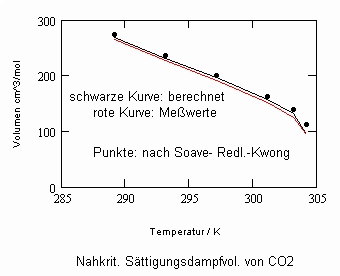
Die erheblichen Genauigkeitsunterschiede der Rechnungen auf der Grundlage kritischer Phänomene und der aus der klassischen van der Waals- Thermodynamik entstandenen Redlich- Kwong- Gleichung vor allem im Flüssigkeitsbereich sind ersichtlich.
Für einige weitere technisch und ökologisch wichtige Stoffe seien die mit Berücksichtigung kritischer Phänomene berechenbaren v‘, v“- Werte angegeben, für die allerdings keine in allgemein zugänglichen Datensammlungen bestehenden (unentgeltlichen) Meßwerte erkennbar waren.
Die Nachrechnungen für Ozon O3 ( Tk = 261.1 K, pk = 5.53 MPa, vk = 89.3818 cm^3/mol) auf der Grundlage kritischer Phänomene für nahkritische Zustände ergeben für die Sättigungsvolumina von Flüssigkeit und Dampf die Diagramme
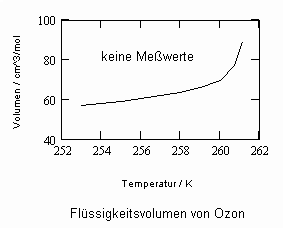 ,
,
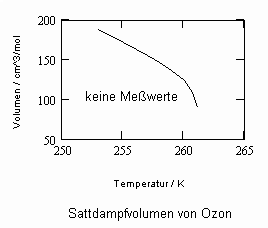 .
.
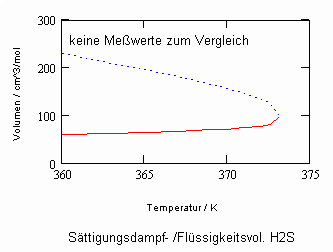
Auch für Schwefelwasserstoff H2 S (Tk = 373.15 K, pk = 8.937 MPa, vk = 98.5029 cm^3/mol) als Ausgangsstoff wichtiger Synthesen waren für nahkritische Zustände keine unentgeltlich zugänglichen Meßwerte verfügbar. Die auf der Grundlage kritischer Phänomene berechneten Daten sind folgende:
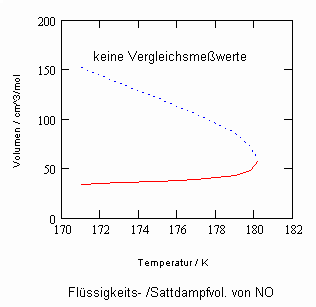
Daten für Stickstoffmonooxid NO kurz unter der kritischen Temperatur (Tk = 180.2 K, pk = 6.485 MPa, vk = 57.7038 cm^3/mol) sind bei Berücksichtigung kritischer Phänomene folgende:
Zu betonen ist, daß zur Ausführung der Rechnung nicht der jeweilige Dampfdruck, doch aber die Angaben zum kritischen Punkt bekannt sein müssen.
Nachdem die Sättigungsvolumina v‘, v“ für eine Temperatur nahe der kritischen Tempertur berechnet sind, kann nun das Flüssigkeits- und Gasverhalten für nahkritische Temperaturen mit z. B. der für reale Gase aus der Theorie kritischer Phänomene abgeleiteten Gleichung
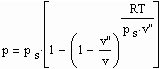
nachgerechnet werden. Allerdings ist nun auch die Kenntnis des Dampfdrucks erforderlich (zur Dampfdruckberechnung s. Artikel vom 11.12.2009 „Die Berechnung von Dampfdrücken“ ).
Als ein Beispiel hierzu sei die Nachrechnung der Realgasfaktoren Z = pv/RT für Wasser bei einer Temperatur von 350 °C (Tk = 374 °C ) und 20 MPa bis zu dem hohen Druck von 100 MPa genannt. Das nachfolgende Diagramm zeigt das Ergebnis der Nachrechnung.
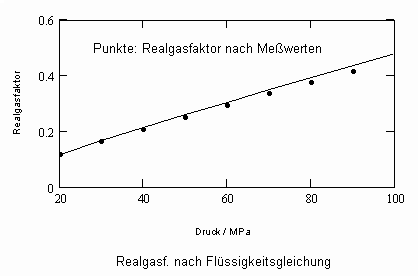
Die gute Übereinstimmung mit den aus Meßwerten berechneten Realgasfaktoren ist ersichtlich. Wird die Rechnung mit einer der üblichen Zustandsgleichungen ausgeführt, sind die Ergebnisse von den Meßwerten viel weiter entfernt- wie das folgende ebenfalls für Wasser bei 350 °C geltende Diagramm entsprechend der Soave- Redlich- Kwong- Gleichung zeigt.
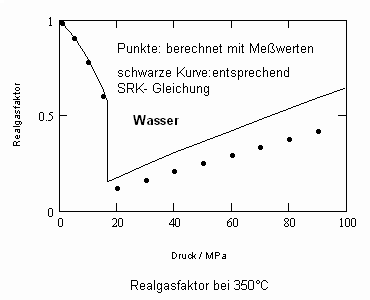
Vor allem für Flüssigkeitszustände sind die Ergebnisse mit der Soave-Redlich-Kwong- Gleichung sehr ungünstig. Für den Gaszustand allerdings stimmen Realgasfaktor-Ergebnisse aus der herkömmlichen Soave- Redlich-Kwong- Gleichung und den sich aus der Theorie kritischer Phänomene ergebenden Werten oft gut mit Werten aus Messungen überein.