Es wird viel von Kernschmelze in Atomkraftwerken gesprochen. Der Anlaß ist die drohende oder schon stattfindende Kernschmelze in Atomkraftwerken Japans.
Nähere Überlegungen zu den Vorgängen einer Kernschmelze sind sehr angebracht.
Bei einer Kernschmelze handelt es sich letzlich um die immer größere gefährliche Aufheizung schmelzender Brennstäbe infolge ungenügender Kühlung bei sich fortsetzender nuklearer Reaktion (Eigenwärme).
Beteiligte Materialien sind oft
– Zirkonium als Umhüllung der Brennstäbe (Schmelzpunkt 1857 °C)
– Urandioxid UO2 (Schmelzpunkt 2827 ° C ) und Plutoniumdioxid PuO2 ( Schmelzpunkt 2400 ° C ) als radioaktive Metalloxide und Füllung der Brennstäbe.
Zur Schmelze kommt es also erst, nachdem die Temperatur im Reaktor bereits bedenklich äußerst hoch bis zu ca. 2000 ° C gestiegen ist.
Eine wichtige Frage ist: Kann man die Vorgänge bei einer eintretenden und sich weiter entwickelnden Kernschmelze überhaupt nachrechnen? Existieren physikalisch begründete und gangbare Berechnungsmöglichkeiten zur Einschätzung des Verlaufs einer Kernschmelze? Es handelt sich ja um Vorgänge radioaktiver flüssiger Stoffe sehr hoher Temperatur, deren Temperatur immer noch zunehmen kann.
Grundlegende Vorausetzung solcher Berechnungsmöglichkeiten ist die Kenntnis der thermophysikalischen Eigenschaften der beteiligten Stoffe nicht nur als Feststoff, sondern auch als Flüssigkeit und bei ihrer Verdampfung. Sind diese Daten ( Dampfdruck als Temperaturfunktion, Flüssigkeits- und Dampfdichte als Temperaturfunktion ) überhaupt als Meßwerte bei solch hohen Temperaturen bekannt und bis zu welchen Temperaturen?
Übliche und allgemein (ohne Gebühr ) zugängliche Stoffdatensammlungen stellen die erforderlichen Angaben für Urandioxid, Plutoniumdioxid, Zirkonium u.a. beteiligte Stoffe nicht zur Verfügung. Auch Literaturstellen zu hochschmelzenden Metallen im flüssigen Zustand bestätigen das eigentlich noch nicht ausreichende Wissen über flüssige Metalle und ihre Verbindungen (s. z.B. für Uran: H. Hess, H. Schneidenbach: Vapour Pressure and critical Data for Uranium, Z. Metallkunde 92,2001).
Es ist allerdings darauf zu verweisen, daß mit den in diesem Blog dargelegten Theorie – Ergebnissen zur Berechnung von Flüssigkeitsvolumina v‘, von Sattdampfvolumina v“ und auch von Dampfdrücken die grob näherungsweise Einschätzung dieser Stoffwerte für an Kernreaktionen und Kernschmelzen beteiligte Substanzen evtl. möglich wird. Nähere Erläuterungen dazu sind in den Artikeln dieses Blogs zu finden:
-Flüssige Metalle, 12.11.2010
-Die Berechnung von Dampfdrücken, 11.12.2009
-Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene, 7.5.2009
-Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene, 1.5.2009.
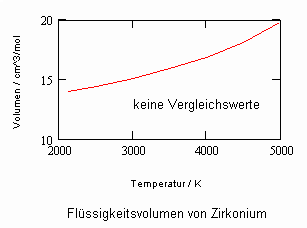
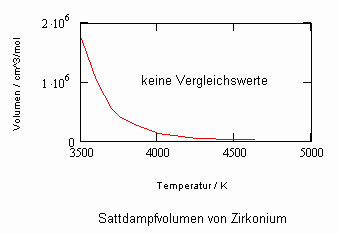
Die nachfolgenden Diagramme geben die Ergebnisse bisheriger Nachrechnungen der Volumina v‘,v“ für Zirkonium, Plutoniumdioxid und Plutonium, die mit den verfügbaren Daten und den o.gen. Mitteln möglich waren, an (Uran s. den Blog- Artikel vom 30.11.2010 ).
Zirkonium Zr: berechnete kritische Temperatur 6540 K.
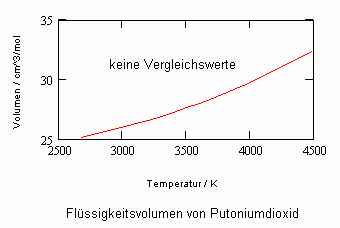
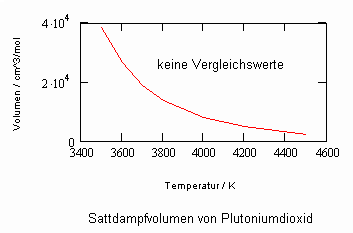
Plutoniumdioxid PuO2,
berechnete kritische Temperatur ca.5950 K
Plutonium Pu, berechnete kritische Temperatur ca. 6935 K
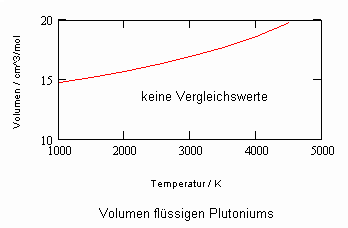
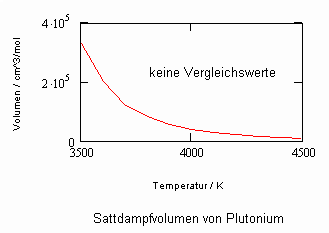
Leider standen zur Nachrechnung der v‘, v“, ps- Daten nur wenige Meßwerte zur Verfügung. So war es z. B. nicht möglich für Urandioxid UO2 die notwendigen Angaben zur Berechnung dieser Daten auf einem einfachen und unentgeltlichen Weg zu beschaffen.
(Neben den gen. allgemein zugänglichen Stoffdatensammlungen wurden benutzt: www.webelements.com; http://i-systems.dechema.de/detherm; David R. Lide: CRC Handbook of Chemistry and Physics, 90 th Edition,CRC Press,Boca raton, Florida 2009; Lester R. Morss,Norman N. Edelstein,jean Fuger: The Chemistry of the Actinide and Transactinide Elements,Spinger,Dortrecht 2006)
Es ist festzustellen: Bei einer etwas verbesserten Datenlage mit v‘ und Dampfdruck- Meßwerten beim Schmelzpunkt und etwas darüber (oder evtl. sogar v‘- Meßwerten bis zum oder beim normalen Siedepunkt) läßt sich der v‘, v“, ps- Verlauf in Abhängigkeit von der Temperatur mit geringeren Fehlern mit den o. gen. Mitteln auf der Grundlage der physikalischen Theorie kritischer Phänomene einschätzen. Damit könnte man dann evtl. begründet versuchen, Modellvorstellungen des Verlaufs einer Kernschmelze zu denken.