Die in diesem Blog gen. und in einzelnen Artikeln beschriebenen neuen Möglichkeiten der Berechnung thermophysikalischer Daten von Flüssigkeiten und Gasen wurden durch eine Erweiterung der für nahkritische Zustände geltenden Gesetze kritischer Phänomene auf vom kritischen Punkt weit entfernte Zustände gewonnen.
Kritische Phänomene sind in einem engen Bereich der Temperatur oder des Drucks nahe der kritischen Daten untersucht und mit ihren kritischen Exponenten erklärt (s. Artikel vom 1.5.2009 „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ und die Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ – ISBN 978-3-00-027253-0) . In der physikalischen Literatur ist die Wirkung kritischer Phänomene auf Zustandsdaten von Stoffen begrenzt auf sehr nahkritische Verhältnisse- bis einige wenige Kelvin der Temperatur T unter bzw. über der kritischen Temperatur Tk oder nur nahe am kritischen Druck pk. So z. B. heißt es: „Man spricht von kritischen Phänomenen. Ihre Universalität erklärt das heftige Interesse an diesen Phänomenen, obwohl sie sich nur im Bereich der kritischen Fluktuationen, also in einem nur sehr schmalen Temperaturbereich abspielen.“ (Nolting: Grundkurs Theoretische Physik 6, Statistische Physik, Springer 2004.)
Mit den vorliegenden Ergebnissen zumindest für die kritischen Phänomene
– Dichtesprung ρ‘-ρ“ zwischen flüssiger und dampfförmiger Phase im Sättigungszustand
– Differenz vom Druck p zum kritischen Druck pk bzw. von der Dichte ρ zur kritischen Dichte ρk auf der kritischen Isotherme Tk
scheint das aber nicht so zu sein!
Denn es zeigt sich, daß die Proportionalitäten zwischen der Dichtedifferenz ρ‘-ρ“ und (Tk-T)^β (für T<Tk) bzw. p-pk und sign(ρ-ρk)(⁄ρk-ρ⁄)^δ keineswegs nur in der unmittelbaren Nähe des kritischen Punktes gelten. Der Beleg dafür ist die Anwendbarkeit der Gleichungen
![]()
und
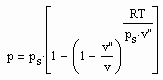 ,
,
die ja erst durch die Erweiterung der gen. beiden kritischen Phänomene auf weit von der kritischen Temperatur entfernte Temperaturen gewonnen werden konnten (ps- Dampfdruck, Kv- sogen. Dichtesprungfaktor), (s. o. gen. Artikel vom 1.5.2009 ). Die gen. beiden Gleichungen gelten trotz ihrer Ableitung aus Gesetzmäßigkeiten kritischer Phänomene keineswegs nur in der unmittelbaren Nähe des kritischen Punktes eines Stoffes. Sie können- wie in den verschiedenen Artikeln dieses Blogs aufgezeigt- durchaus zur näherungsweisen Berechnung von Stoffdaten benutzt werden. Die physikalische Theorie hierzu und die Ableitung dieser und weiterer Gleichungen ist in der o.gen. Veröffentlichung ausführlich dargelegt.
Entsprechend der Universalitätshypothese von Griffiths (R.B. Griffiths, Phys. Rev. Lett. 24, 1479 (1970)) haben die kritischen Exponenten für völlig verschiedene Stoffe fast die gleichen Werte (s. z. B. Nolting: „Grundkurs Theoretische Physik 6, Statistische Physik“, Springer Verlag 2004). Diese sehr erstaunliche Eigenschaft der verschiedensten Stoffe trifft zu- aber eben doch nur fast!
Theoretische Physiker erklären die Universalitätshypothese als unterdessen bewiesen entsprechend der Renormierungsgruppentheorie von K. Wilson.
Damit ist letztlich gesagt, daß die Universalitätshypothese selbst für Stoffe komplizierter chemischer Strucktur zutreffen muß- also nicht nur für Stoffe einfacher Moleküle (wie N2,O2, Ar, He, H2 usw.), für die die meisten Messungen vorliegen, sondern auch für Stoffe größerer Molekülmasse mit z.B. C- Doppelbindungen, aromatischen Ringen, Heterocyclen und der ungeheuren Vielzahl weiterer anorganischen und organischen Verbindungen.
Die Frage,ob das angesichts der überwältigenden Vielfalt von Stoffen immer so entsprechend der Universalitätshypothese tatsächlich ist ( sie selbst formuliert die Einschränkung „fast“ ), muß wohl erlaubt sein. Denn es ist zu bedenken, daß notwendige Untersuchungen und Messungen mit geringer Fehlertoleranz in der Nähe des kritischen Punktes schwierig sind. Nur für relativ wenige Stoffe liegen z.B. p,v- Messungen auf der kritischen Isotherme vor.
Wenn die Universalitätshypothese von einer nur „fast“ zutreffenden Universalität der kritischen Exponenten spricht, ist offensichtlich eine Variabilität dieser Exponenten im Rahmen der Vielfalt unterschiedlicher Stoffe zugelassen. Es ist zu fragen, ob für diese Variabilität die Ungenauigkeit der schwierigen Messung verantwortlich ist oder ob der jeweilige kritische Exponent doch etwas vom Stoff abhängig ist. Auch Nachfragen dazu bei namhaften theoretischen Physikern konnten diese Frage nicht völlig klären. Teilweise wurde auf immer feste Werte der kritischen Exponenten verwiesen, teilweise wurde die Variabilität bei komplizierteren Molekülen und bei veränderten sogen. Universalitätsklassen benannt.
Keineswegs ist es so, daß die Variabilität kritischer Exponenten nur klein ist. Sehr deutlich zeigt sich das an dem kritischen Phänomen,welches den nahkritischen Zusammenhang von Druck und Dichte auf der kritischen Isotherme beschreibt. Für den dazu in der physikalischen Literatur benannten kritischen Exponenten δ wird immerhin ein beträchtlicher Wertebereich von 4 bis 4.8 genannt. Eine weit geringere Streuung der festgestellten Werte des kritischen Exponenten besteht für das kritische Phänomen, das den nahkritischen Dichteverlauf in Abhängigkeit von der Temperatur mit dem in der physikalischen Literatur bezeichneten Exponenten β beschreibt. Die Werte für β streuen nur von 0.33 bis 0.37. Obwohl der versuchstechnische Nachweis und die Gültigkeit des mit dem kritischen Exponenten β verbundenen kritischen Phänomens der Proportionalität der Dichtedifferenz ρ‘-ρ“ mit der Temperaturdifferenz entsprechend (Tk-T)^β nur für Temperaturen in unmittelbarer Nähe der jeweiligen kritischen Temperatur erklärt ist, ergab sich der Nachweis dafür, daß die gen. Proportionalität auch für Zustände weit entfernt von der kritischen Temperatur gilt. Der Ausdruck dafür ist die bereits o. gen. Gleichung
![]() ,
,
die die Grundlage wesentlicher Stoffdatenberechnungen der Artikel dieses Blogs und der Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen – berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0) ist. Wirklich interessant ist, daß diese Gleichung , obwohl sie eigentlich nur für jeweils sehr nahkritische Temperaturen gelten dürfte, tatsächlich für die verschiedensten Stoffe auch komplizierten Molekülaufbaues sehr weit entfernt von der kritischen Temperatur anwendbar ist. Die Frage, warum das so ist , ist letzlich von der heutigen Theoretischen Physik unbeantwortet.
Die Theorie kritischer Phänomene erklärt die Eigenschaften bestimmter physikalischer Größen als eine Reihenentwicklung der reduzierten Temperatur (Tk-T)/Tk. Auch für die Dichtedifferenz ρ‘-ρ“ besteht solch eine Reihenentwicklung. Damit ist es dann möglich, eine sehr genaue Gleichung zur Bestimmung der Siededichte eines Stoffes als Temperaturfunktion abzuleiten, wenn nur einige wenige Meßwerte dazu vorliegen (s. den Artikel vom 5.7.2010 in diesem Blog “ Kritische Exponenten als mögliche Grundlage sehr genauer Stoffwertberechnungen“). Beispielrechnungen bei hoher Übereinstimmung mit Meßwerten wurden mit dem kritischen Exponenten β = 1/3 durchgeführt.
Die o.gen. Zustandsfunktion
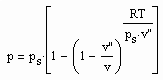
wurde mit einer Erweiterung des für den Druck und der Dichte auf der kritischen Isotherme geltenden kritischen Phänomens des Exponenten δ = 4.4±0.4 abgeleitet. Voraussetzung dabei ist die Hypothese, daß das für die kritische Isotherme erklärte kritische Phänomen
![]()
(const- Konstante) auf Drücke weit entfernt vom kritischen Druck und auch auf Temperaturen entfernt von der kritischen Temperatur übertragen werden kann. Die mathematische Strucktur der sich mit dieser Hypothese ergebenden Gleichungen führt dann allerdings nicht zu dem Exponenten δ, sondern zu einem Exponenten RTk/pkvk für die kritische Isotherme bzw. zu RT/psv“ für eine von Tk verschiedene Temperatur.
Interessant ist, daß dieser sich aus der Rechnung ergebende Exponent der reziproke Wert des in der Technischen Thermodynamik verwendeten Realgasfaktors eines Gases im Sättigungszustand ist: ps v“/RT. Auf der kritischen Isotherme liegen Werte des reziproken Realgasfaktors für alle möglichen Stoffe oft bei 3.5 bis 4.5- also durchaus in der Größenordnung des kritischen Exponenten δ= 4.4±0.4. Wenn bedacht wird, daß der kritische Exponent um 4.4 nur auf der kritischen Isotherme in der unmittelbaren Nähe des kritischen Drucks gilt, ist der Unterschied zum reziproken Wert des Realgasfaktors evtl. durch die Erweiterung des kritischen Phänomens auf Drücke keineswegs nur in der Nähe des kritischen Drucks erklärbar. Die näherungsweise Gültigkeit der abgeleiteten o. gen. Zustandsfunktion ist durch eine Vielzahl von Nachrechnungen bei Vergleichen mit Meßwerten nachgewiesen. Sie hat den Vorteil, unabhängig von empirischen Voraussetzungen zu sein- z. B. von dem in der Technischen Thermodynamik für sogen. halbempirische Zustandsgleichungen notwendigen völlig empirischen azentrischen Faktor.
Die bisherigen Untersuchungen zur Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene auf Daten weiter entfernt von Daten des kritischen Punktes sind bisher nur auf die o.gen. kritischen Phänomene bezogen. Ergebnisse zur Kompressibilität und vor allem zur der Wärmekapazität eines Stoffes als Funktion der Temperatur liegen noch nicht vor; sie sind in Arbeit, um festzustellen, ob auch dafür Gesetzmäßigkeiten kritischer Phänomene im beschriebenen Sinne modifiziert werden können.