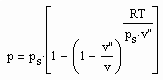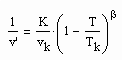Die Auswertung von Gesetzmäßigkeiten kritischer Phänomene, die von der Theoretischen Physik abweichend von der sonst üblichen van der Waals- Thermodynamik festgestellt sind, ergab eine Zustandsfunktion als Zusammenhang zwischen Druck p, Volumen v und Temperatur T der Form
Dabei ist ps der Dampfdruck und v“ das Sättigungsdampfvolumen.
Im Ergebnis der Untersuchungen zu Siededaten von Stoffen, die aus Gesetzmäßigkeiten kritischer Phänomene ableitbar sind, ergab sich für weitab von der kritischen Temperatur befindliche Temperaturen die grob näherungsweise bestehende Beziehung
Dabei ist β der kritische Exponent mit dem Betrag 1/3 , Tk ist die kritische Temperatur , vk das kritische Volumen und v‘ das Siedevolumen bei einer weit von der kritischen Temperatur entferntenTemperatur. Die Größe K erweist sich dabei als eine dimensionslose allgemeine Konstante der Größenordnung grob allgemein von 3.7 (in einem Variationsbereich von 3 bis 4- oft also bei 3.7) (s. Tampe. F. : „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“- ISBN 978-3-00-027253-0). Es ist also immer möglich, das Flüssigkeitsvolumen v‘ eines Stoffes für weitab von der kritischen Temperatur entfernte Temperaturen einzuschätzen- selbst wenn nichts weiter außer den Daten des kritischen Punktes bekannt ist. Damit erweist es sich dann letztlich als möglich, nahkritische pvT- Stoffdaten als Näherung zu berechnen (s. die Artikel „Die Anwendbarkeit krit. Phänomene zur Berechnung von pvT- Daten“ vom 23.2.2013, „Mitteilung zu Zustandsgleichungen für reale Gase und Flüssigkeiten- abgeleitet aus der Theorie kritischer Phänomene“ vom 16.11.2012, „Zur Berechnung nahkritischer Stoffdaten von Flüssigkeiten und Gasen“ vom 1.7.2012).
In sehr vielen Fällen sind pvT- Daten von Stoffen in der Umgebung des jeweiligen normalen Siedepunkts vom Tripelpunkt bis zu höheren Temperaturen bekannt. Es kann aber auch sein, daß nur die kritischen Daten bekannt sind und sonst fast keine Angaben zu wichtigen Stoffwerten (außer denen z. B. zu Feststoffdaten) vorliegen. Leider ist das oft so- wie Beispiele aus Stoffdatenbanken bzw. web- Informationen zeigen.
Es kann also sehr schwierig oder sogar unmöglich werden, Stoffdaten allein durch Rechnung bestimmen oder einschätzen zu wollen, wenn nur wenige Meßwerte bekannt sind- z. B. in all den Fällen bei allein nur bekannten kritischen Daten. Die Situation ist allerdings verbessert, wenn die nun bekannten Veränderungen durch die festgestellte Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene auch auf Temperaturen weit ab von der kritischen Temperatur beachtet werden.
Für all diese Fälle, deren Stoffdaten bei allein nur bekannten kritischen Daten zumindest als grobe Näherung mit Gesetzen kritischer Phänomene bestimmt werden können, sollen nachfolgend einige interessante Beispiele dargelegt werden.
Ein seit vielen Jahren wichtiger Stoff bei der Isotopentrennung von Uran 235 und Uran 238 ist Uranhexafluorid UF6, wobei die Trennung in Gaszentrifugen geschieht. Das technische know how dieses Prozesses ist aus verständlichen Gründen keineswegs völlig offen. Auch die Stoffdaten sind in allgemein zugänglichen Datensammlungen der Literatur und Datenbanken des web nur teilweise zugänglich.
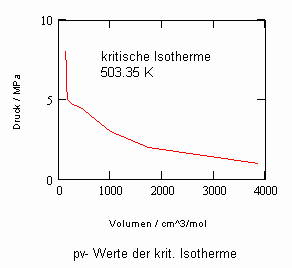
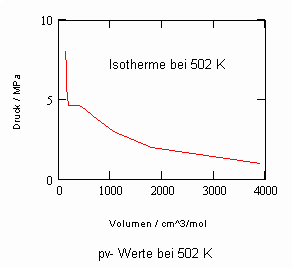
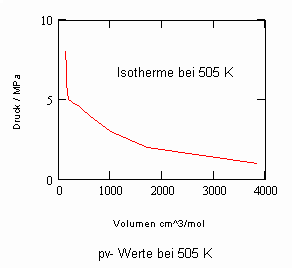
Verfügbar sind z. B. die Daten des kritischen Punktes: Tk = 503.35 K (230.2 °C), pk = 4.66 MPa, vk = 256 cm³/mol. Allein mit diesen Angaben (und sonst keinen weiteren) ist es nun möglich, mit den sich aus kritischen Phänomenen ergebenden neuen Berechnungsgleichungen die pvT- Daten der kritischen Region rechnerisch einzuschätzen. Auch die pv-Werte auf Isothermen überkritischer Temperaturen, die sich weiter entfernt von der kritischen Temperatur befinden, können nun so als Näherungen ermittelt werden. Die nachfolgenden Diagramme, die pv- Daten für nahkritische Temperaturen angeben, sind das Ergebnis solcher nun möglicher Rechnungen für Uranhexafluorid.
Rechnungen für technisch relevante pvT- Daten von UF6 erweisen sich nun als durchaus möglich!
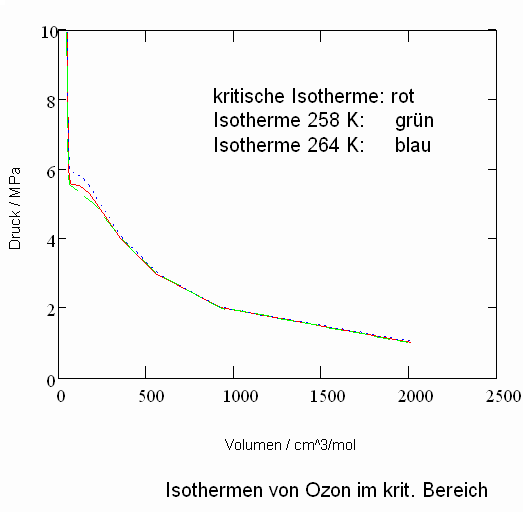
Ein weiteres Beispiel eines wichtigen Stoffes mit nur unvollständigen Angaben in frei verfügbaren Datenbanken ist Ozon O3. Angegeben werden i.a. die kritischen Daten für Temperatur, Druck und Volumen Tk = 261.05 K, pk = 5.46 MPa, vk = 89.38 cm^3/mol. Auch der normale Siedepunkt bei 161.25 K und der Tripelpunkt bei 80.45 K wird genannt.
Allein mit solchen Angaben ist es nun auf der Grundlage der gen. Gesetzmäßigkeiten kritischer Phänomene möglich, pvT- Daten in der kritischen Region und darüber hinaus zu berechnen. Für Ozon z. B. ergeben sich so die folgenden Diagramme für Isothermen in der kritischen Region.
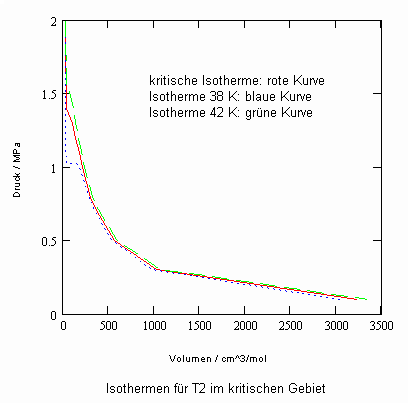
Ein anderes interessantes Beispiel zur Erfassung von pvT-Daten in der kritischen Region ist Tritium T2. Das Molekül besteht aus zwei Tritium- Atomen, wobei der Tritiumkern selbst aus zwei Protonen und einem Neutron besteht. Die folgenden Daten werden in internationalen Datenbanken genannt: Tk = 40.55 K, vk = 57.0576. Der normale Siedepunkt wird mit 25.03 K angegeben.
Für Tritium T2 können als Näherung die folgenden pvT- Daten in der kritischen Region entsprechend folgenden Diagramms berechnet werden:
Für viele weitere Stoffe können nun was hier gezeigt werden sollte- bei bekannten kritischen Daten näherungsweise pvT- Angaben für das kritische Gebiet und auch weit darunter bzw. darüber berechnet werden!