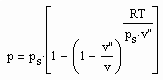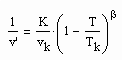Veröffentlichungen
September 6th, 2014
Veröffentlichungen
September 6th, 2014
Die nun einfache Möglichkeit der Berechnung von pvT-Daten in der kritischen Region eines Stoffes
März 28th, 2014
Zur Berechnung von Stoffwerten für Flüssigkeiten und Gase in der kritischen Region von Stoffen
Januar 23rd, 2014Ganz allgemein ist ja leider festzustellen, daß alle bisherigen in der chemischen Technik und Verfahrenstechnik angewendeten Zustandsgleichungen, selbst die modernsten, nicht in der Lage sind, die realen pvT- Verhältnisse eines Stoffes mit ausreichender Genauigkeit in der kritischen Region darzustellen. Das bestätigen Aussagen zur Genauigkeit in der kritischen Region z. B. auch in der wichtigen und modernen web- site „nist webbook“, die pvT- Werte oft angewendeter Stoffe der chemischen Industrie mit den aktuell besten empirischen Zustandsgleichungen nach Anpassung an Meßwerte angibt (s. auch den Artikel „Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region“ vom 15.4.2013). Auch die Erwartung, daß sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne oder geringe empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Mit nun vorliegenden Untersuchungsergebnissen zum pvT- Verhalten reiner Stoffe in der kritischen Region ist versuchsweise ein Theorie- Ansatz abgeleitet worden, der zu einer Erweiterung von Gesetzmäßigkeiten kritischer Phänomene weit über ihre bisherige Anwendbarkeit begrenzt auf die nahe Umgebung des kritischen Punktes führt. So ergeben sich z. B. Berechnungsgleichungen für die kritische Isotherme und benachbarte Isothermen, die die pvT- Verhältnisse in der Nähe des kritischen Punktes eines Stoffes allein nur bei Kenntnis der kritischen Daten pk, vk, Tk bei guter Annäherung an die Realität wiedergeben. Allerdings ist dieser Ansatz außerhalb des bisherigen Main- Streams. Die von manchen theoretischen Physikern vertretene Ansicht, kritische Exponenten seien analog einer Naturkonstanten unabhängig vom Stoff und etwa konstant, bestätigt sich mit diesem Theorie- Ansatz nur teilweise. Der kritische Exponent β bestätigt sich stoffunabhängig mit ca. 1/3, der Exponent δ allerdings erweist sich als stoffabhängig berechenbar mit den kritischen Daten.
Die van der Waals- Thermodynamik und die vielen auf dieser Grundlage abgeleiteten Zustandsgleichungen gelten ja nicht in der kritischen Region. Hier gelten die Gesetzmäßigkeiten kritischer Phänomene, deren Wirksamkeit nachgewiesen und von der Theorie her erklärt ist- aber doch noch nicht soweit entwickelt ist, dass man für technische Zwecke verlässlich damit rechnen könnte. Veröffentlichte Stoffwerte für Zustände in der kritischen Region können deshalb mit erheblichen Fehlern behaftet sein, wie die Autoren von Stoffwertdaten selbst einschätzen. Die Situation der Bestimmung von Zustandsdaten in der Umgebung des kritischen Punktes eines Stoffes ist bereits in verschiedenen Artikeln dieses Blogs näher dargestellt: „Die Anwendbarkeit kritischer Phänomene zur Berechnung von pvT- Daten“ vom 23.2.2013; „Zur Genauigkeit der Berechnung von pvT-Daten in der kritischen Region“ vom 15.4.2013. Die in Datensammlungen und in der Literatur beschriebenen Berechnungsgrundlagen beziehen sich auf supergenaue Messungen in der kritischen Region und auf jeweils weitgehende empirische Zustandsgleichungen für technisch wichtige Stoffe. Allgemeingültige Lösungen ausreichender Genauigkeit können nicht genannt werden.
Nun ergab es sich nach den o. gen. speziellen Untersuchungen des Verhaltens von Stoffen in der kritischen Region, dass eine Hypothese zur näherungsweisen Erweiterung des Gültigkeitsbereichs kritischer Phänomene sowohl für Zustände um den kritischen Punkt als auch für Zustände weiter entfernt vom kritischen Punkt zu der Realität weitgehend nahekommenden Ergebnissen führt (Angaben zur Theorie und ihre Anwendungen s. z. B. den Artikel „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ vom 1.5. 2009). Nachrechnungen der pv- Daten kritischer Isothermen gut vermessener Stoffe zeigen das, indem die Berechnungsergebnisse entsprechend der neuen zur Theorie kritischer Phänomene abgeleiteten Möglichkeiten mit Ergebnissen von bisher angewendeten Zustandsgleichungen- dokumentiert in „nist webbook“- verglichen werden. Zu betonen ist, dass zur Bestimmung der pv-Werte auf der kritischen Isotherme entsprechend der neuen Berechnungsmöglichkeiten nur die Kenntnis der kritischen Daten pk, vk, Tk notwendig ist, während die von renommierten Autoren angewendeten weitgehend empirischen Zustandsgleichungen umfangreiche Messungen und Anpassungen erfordert haben. Beispiele zum Vergleich der Ergebnisse des neuen Theorie- Ansatzes mit denen nach herkömmlichen weitgehend empirischen Zustandsgleichungen renommierter Autoren auf der Grundlage sehr genauer Messungen und Anpassungen können nach Anforderung (dr.f.tampe@t-online.de) zur Verfügung gestellt werden (für Benzol, Toluol, Ethylen, Kohlenstoffdioxid, Propylen, Helium, Wasserstoff, Methanol…usw.). Auch verwendbare Nachrechnungen für pvT- Daten von Stoffen, zu denen keine Meßwerte außer denen der kritischen Daten in der kritischen Region existieren, sind nun vorstellbar! Das ist durchaus für bisher nicht weiter vermessene Stoffe bei nur der Kenntnis der kritischen Daten zu erwarten (entsprechende Anfragen ebenfalls an die o.gen. Mail- Adresse bei kostenloser Bearbeitung, falls die Ergebnisse nach Absprache zur Auswertung benutzt werden dürfen).
Sehr interessant ist es auch, dass es mit den neuen Möglichkeiten zur Berechnung von pv- Daten auf Isothermen möglich ist, die Sättigungsdaten v‘, v“ von Flüssigkeiten und Dämpfen entsprechend der Temperatur als Näherungen zu bestimmen. Für die v‘-, v“-Volumina von Stoffen kurz unter der kritischen Temperatur eines Stoffes und weiter entfernt von der kritischen Temperatur können so Berechnungsgleichungen abgeleitet werden. Diese Gleichungen geben die Sättigungsvolumina von Flüssigkeiten und Dämpfen als Temperaturfunktion und als Näherung an. Die Genauigkeit der Flüssigkeitsdaten ist dabei oft recht hoch und entsprechend von Meßwerten erheblich besser als die der Dampfdaten. Anfragen zu solchen Nachrechnungen o. gen. Art sind möglich. Es ist darauf hinzuweisen, daß es bisher keine allgemein gültige Möglichkeit gibt, die Sättigungsvolumina von Stoffen als Näherung zu berechnen.
Gedanken zur physikalischen Begründung der heutigen Thermodynamik für Gemische
Dezember 15th, 2013Die zentrale und technisch wichtigste Aufgabe der Thermodynamik von Gemischen ist die Ermöglichung von Phasengleichgewichtsberechnungen.
In technisch vielen Fällen ist ein Flüssigkeitsgemisch mit vorgegebenen Konzentrationen verschiedener Substanzen bei einer vorgegebenen Temperatur der Ausgangspunkt der Berechnungen. Das Ziel der Rechnung ist dann die Bestimmung der dem Siedegleichgewicht entsprechenden Dampfkonzentrationen und des Siededruckes.
Zu dieser zentralen Aufgabe der Gemischthermodynamik existiert eine unglaubliche Vielzahl von Theorien, Methoden und empirischen Vorgehensweisen, die trotz aller praktischen Erfolge leztlich immer noch nicht zu physikalisch begründeten ohne wesentliche Empirie- Anteile auskommenden Berechnungsgleichungen geführt haben.
Die theoretischen Ausgangspunkte von Phasengleichgewichtsberechnungen sind
-Zustandsgleichungen für Gemische und sogen. -Aktivitätskoeffizienten- Modelle.
Grundlage der Rechnung ist immer die Feststellung der partiellen molaren Freien Enthalpie jeder Komponente des Gemisches, denn Gleichgewicht besteht dann, wenn die partiellen Freien Enthalpien der Komponenten in verschiedenen Phasen des Gemisches übereinstimmen.
Alle heute in der Gemischthermodynamik gebräuchlichen Zustandsgleichungen sind letzlich von der physikalisch begründeten van der Waals- Zustandsgleichung, der Virial- Gleichung und Ansätzen der Statistischen Thermodynamik abgeleitet. In vielen technisch wichtigen Fällen sind Weiterentwicklungen der klassischen van der Waals- Gleichung Ausgangspunkt von Phasengleichgewichtsberechnungen geworden. So z. B. die Soave- Redlich-Kwong- Gleichung und die Peng- Robinson- Gleichung, die ausgehend von ihrer für reine Stoffe erklärten Formulierung auch auf Stoffgemische ausgedehnt wurden. Allerdings sind diese Weiterentwicklungen mit erheblichen empirischen Anteilen verbunden, die sich sowohl auf den reinen Stoff als auch auf das Gemisch beziehen. So wird zur besseren Anpassung der Zustandsgleichung an das Realverhalten der Reinstoffe ein sogen. azentrischer Faktor ω eingeführt, der theoretisch fundiert nicht bestimmt werden kann, sondern mit Meßwerten und ausgeprägt empirisch für jeden Stoff zu ermitteln ist. Der empirische Anteil zur Beschreibung der Gemischeigenschaften in heute gebräuchlichen Gemischzustandsgleichungen der Technischen Thermodynamik ist erheblich. Er zeigt sich besonders in dem Teil der Zustandsgleichungen, die den Einfluß der molekularen Wechselwirkungen der Gemischbestandteile darstellen. Das geschieht dann so, daß für jede mögliche Stoffkombination einer Mischung spezielle Parameter der Zustandsgleichung durch Laborversuche festzustellen sind.
Bei der praktischen Anwendung von Gemischzustandsgleichungen ergibt es sich oft, daß das pvT- Verhalten gerade der flüssigen Phase zu ungenau erfaßt ist. Die Berechnung der partiellen Freien Enthalpie zur Bestimmung des Stoffgleichgewichts ist dann ebenfalls viel zu ungenau. Zur Beschreibung flüssiger Gemischphasen werden deswegen heute sogen. Aktivitätskoeffizienten- Modelle angewendet, die es gestatten, sogen. Aktivitäten und damit letzlich die partiellen Freien Enthalpien der Komponenten in der Flüssigkeit mit einer höheren Genauigkeit anzugeben. Ansätze dieser Art sind z.B. die Wilson-, die NRTL- und die UNIQUAC- Gleichung (Wilson, G.M. (1964), J. AM. Chem. Soc. 86 , 127; Renon, H., Prausnitz, J.M. (1968), AIChE J. 21, 116; Abrams, D., Prausnitz, J.M. (1975) AIChE J. 14, 135). Mit solchen Gleichungen gelingt es durchaus, für viele Stoffgemische weitgehend richtige Phasengleichgewichtsberechnungen durchzuführen. Allerdings ist der begriffliche und der empirische Aufwand bei der Anwendung solcher Gleichungen sehr erheblich. So z. B. werden sehr spezielle Daten- wie „relatives van der Waalssches Volumen“, „relative van der Waalssche Oberfläche“ usw. benötigt, die für etliche Reinstoffe empirisch ermittelt in der Literatur vorliegen. Zur Berücksichtigung der Wechselwirkungen zwischen den Molekülen sind weitere spezielle „Wechselwirkungs-Parameter“ definiert, die aus bereits bekannten Phasengleichgewichtsdaten durch Anpassungen erst ermittelt werden müssen. Von einer echten physikalisch begründeten Vorausberechnung des gesuchten Phasengleichgewichts kann also gar nicht die Rede sein, da ja vorher bekannte Gleichgewichtsdaten zur Anpassung andie vorausgesetzten Gleichungen bekannt sein müssen.
Zusammenfassend ist zu sagen, daß der Zwang zur Bereitstellung anwendungsfähiger wenn auch weitgehend empirischer Berechnungsmethoden auf Grund der rasanten chemischen und verfahrenstechnischen Weiterentwicklung der stoffwandelnden Industrie sehr hoch war, so daß die gen. und noch weitere weitgehend empirische Gleichungen zur Phasengleichgewichtsberechnung entstanden sind. Sicherlich ist auch festzustellen, daß die Theoretische Physik bisher nicht inder Lage war, durch Bereitstellung entsprechender Theorie- Vorgaben den Empirie- Anteil wesentlich zu verringern.
Nun ergibt es sich, daß eine ausgehend vom physikalisch begründeten van der Waalsschen Ansatz formulierte Zustandsgleichung für Flüssigkeiten der Variablen p-Druck (MPa), v- Volumen (cm³/mol), T- Temperatur (K)
mit dem Eigenvolumen b (cm³/mol) der Moleküle des Stoffes, einem Parameter K ( der mit dem mit dem Dampfdruck berechenbar ist) und der allgemeinen Gaskonstante R (J/mol K) zu Berechnungsgleichungen für Gemische führt, die es erlauben, Phasengleichgewichte mit einem nur geringen Empirie- Anteil zu bestimmen. Das sogen. Eigenvolumen in obiger Flüssigkeits- Zustandsgleichung erweist sich als berechenbar, wenn nur ein einziger Datenpunkt des jeweiligen Stoffes bekannt ist.
Für Bedingungen niedriger bis mäßiger Drücke führt die Theorie mit obiger Flüssigkeitszustandsgleichung zu relativ einfachen Berechnungsgleichungen des Phasengleichgewichts von Stoffgemischen, die nach ihrer Programmierung per Computer lösbar sind. Man erhält die jeweilige Gemischzustandsgleichung und eine Gleichgewichtsbedingung, die aus der Gleichheit der partiellen Freien Enthalpien der Gemischkomponenten in unterschiedlichen Phasen folgt. Die Formulierung dieser Gleichungen ist nur mit o. gen. Flüssigkeitszustandsgleichung möglich, die das Verhalten von Flüssigkeiten akzeptabel genau beschreibt. So zeigt sich z. B., daß so gar keine „azentrischen Faktoren“ und auch keine sogen. „binären Parameter“, mit denen die Wechselwirkungen zwischen Gemischkomponenten empirisch erfaßt werden müssen, erforderlich sind. Auch die Anwendung der sogen. Aktivitätskoeffizienten- Modelle, die ja weitgehend empirisch formuliert sind, kann so entfallen, da die partiellen Freien Enthalpien bzw. Fugazitäten der Gemischkomponenten ausgehend von einem physikalisch begründeten van der Waals- Ansatz für Gemische dargestellt werden können. Die Theorie dazu und die per Computer programmierbaren Berechnungsgleichungen sind ersichtlich: Tampe, F.:“ Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“, 2009, ISBN 978-3-00-027253-0; „Neue Berechnungsmöglichkeiten thermophysikalischer Daten für reine Stoffe und Gemische“, ISBN 3-00-018582-5, 978-3-018592-2.
Zur Überprüfung der neuen Berechnungsmöglichkeiten wurden exemplarisch binäre und auch ternäre Gemische mit Verhaltensweisen von fast ideal bis hin zu ausgeprägt real untersucht. Es zeigt sich, daß die berechneten Konzentrationen immer einer Näherung im Prozentbereich gegenüber Meßdaten entsprechen. Selbst die Anwendung für extrem reale Gemische- also für Gemische mit Mischungslücke (wie z.B. Wasser- Benzol, Wasser- Butanol, Wasser- Phenol) erweist sich als machbar. Damit ist dann sogar die Berechnung von Löslichkeiten, also z. B. die Berechnung der Löslichkeit von Benzol in Wasser bei guter Übereinstimmung mit Meßwerten möglich.
Die bisher in der technischen Gemisch-Thermodynamik so wichtigen aber weitgehend empirischen Aktivitätskoeffizienten- Modelle sind nun ergänzt durch die Theorie- Schlußfolgerungen für Gemische, die sich aus der o.gen. Flüssigkeitszustandsgleichung ergeben. Aktivitätskoeffizienten können so viel einfacher und ohne spezielle Vorleistungen – wie „relatives van der Waalssches Volumen“, „relative van der Waalssche Oberfläche“ und durch Messungen und Anpassungen zu bestimmende „Wechselwirkungsparameter“ – berechnet werden. Die Theorie dazu und die zur Programmierung erforderlichen Berechnungsgleichungen werden in einer 2014 beabsichtigten Veröffentlichung im Detail dargestellt („Thermodynamik der Flüssigkeiten und realen Gase- alternative Berechnungen mit Gesetzmäßigkeiten kritischer Phänomene“).
Einige interessante Beispiele zur Stoffwertberechnung auf der Grundlage kritischer Phänomene
Mai 7th, 2013Die Auswertung von Gesetzmäßigkeiten kritischer Phänomene, die von der Theoretischen Physik abweichend von der sonst üblichen van der Waals- Thermodynamik festgestellt sind, ergab eine Zustandsfunktion als Zusammenhang zwischen Druck p, Volumen v und Temperatur T der Form
.
Dabei ist ps der Dampfdruck und v“ das Sättigungsdampfvolumen.
Im Ergebnis der Untersuchungen zu Siededaten von Stoffen, die aus Gesetzmäßigkeiten kritischer Phänomene ableitbar sind, ergab sich für weitab von der kritischen Temperatur befindliche Temperaturen die grob näherungsweise bestehende Beziehung
.
Dabei ist β der kritische Exponent mit dem Betrag 1/3 , Tk ist die kritische Temperatur , vk das kritische Volumen und v‘ das Siedevolumen bei einer weit von der kritischen Temperatur entferntenTemperatur. Die Größe K erweist sich dabei als eine dimensionslose allgemeine Konstante der Größenordnung grob allgemein von 3.7 (in einem Variationsbereich von 3 bis 4- oft also bei 3.7) (s. Tampe. F. : „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“- ISBN 978-3-00-027253-0). Es ist also immer möglich, das Flüssigkeitsvolumen v‘ eines Stoffes für weitab von der kritischen Temperatur entfernte Temperaturen einzuschätzen- selbst wenn nichts weiter außer den Daten des kritischen Punktes bekannt ist. Damit erweist es sich dann letztlich als möglich, nahkritische pvT- Stoffdaten als Näherung zu berechnen (s. die Artikel „Die Anwendbarkeit krit. Phänomene zur Berechnung von pvT- Daten“ vom 23.2.2013, „Mitteilung zu Zustandsgleichungen für reale Gase und Flüssigkeiten- abgeleitet aus der Theorie kritischer Phänomene“ vom 16.11.2012, „Zur Berechnung nahkritischer Stoffdaten von Flüssigkeiten und Gasen“ vom 1.7.2012).
In sehr vielen Fällen sind pvT- Daten von Stoffen in der Umgebung des jeweiligen normalen Siedepunkts vom Tripelpunkt bis zu höheren Temperaturen bekannt. Es kann aber auch sein, daß nur die kritischen Daten bekannt sind und sonst fast keine Angaben zu wichtigen Stoffwerten (außer denen z. B. zu Feststoffdaten) vorliegen. Leider ist das oft so- wie Beispiele aus Stoffdatenbanken bzw. web- Informationen zeigen.
Es kann also sehr schwierig oder sogar unmöglich werden, Stoffdaten allein durch Rechnung bestimmen oder einschätzen zu wollen, wenn nur wenige Meßwerte bekannt sind- z. B. in all den Fällen bei allein nur bekannten kritischen Daten. Die Situation ist allerdings verbessert, wenn die nun bekannten Veränderungen durch die festgestellte Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene auch auf Temperaturen weit ab von der kritischen Temperatur beachtet werden.
Für all diese Fälle, deren Stoffdaten bei allein nur bekannten kritischen Daten zumindest als grobe Näherung mit Gesetzen kritischer Phänomene bestimmt werden können, sollen nachfolgend einige interessante Beispiele dargelegt werden.
Ein seit vielen Jahren wichtiger Stoff bei der Isotopentrennung von Uran 235 und Uran 238 ist Uranhexafluorid UF6, wobei die Trennung in Gaszentrifugen geschieht. Das technische know how dieses Prozesses ist aus verständlichen Gründen keineswegs völlig offen. Auch die Stoffdaten sind in allgemein zugänglichen Datensammlungen der Literatur und Datenbanken des web nur teilweise zugänglich.
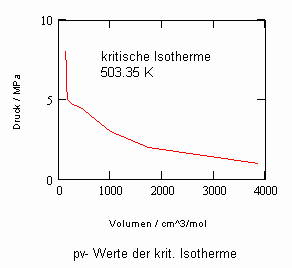
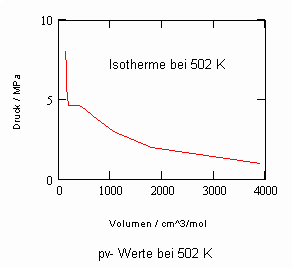
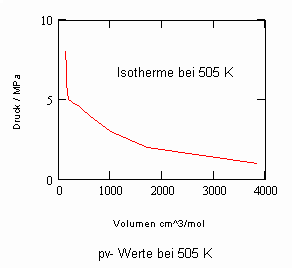
Verfügbar sind z. B. die Daten des kritischen Punktes: Tk = 503.35 K (230.2 °C), pk = 4.66 MPa, vk = 256 cm³/mol. Allein mit diesen Angaben (und sonst keinen weiteren) ist es nun möglich, mit den sich aus kritischen Phänomenen ergebenden neuen Berechnungsgleichungen die pvT- Daten der kritischen Region rechnerisch einzuschätzen. Auch die pv-Werte auf Isothermen überkritischer Temperaturen, die sich weiter entfernt von der kritischen Temperatur befinden, können nun so als Näherungen ermittelt werden. Die nachfolgenden Diagramme, die pv- Daten für nahkritische Temperaturen angeben, sind das Ergebnis solcher nun möglicher Rechnungen für Uranhexafluorid.
Rechnungen für technisch relevante pvT- Daten von UF6 erweisen sich nun als durchaus möglich!
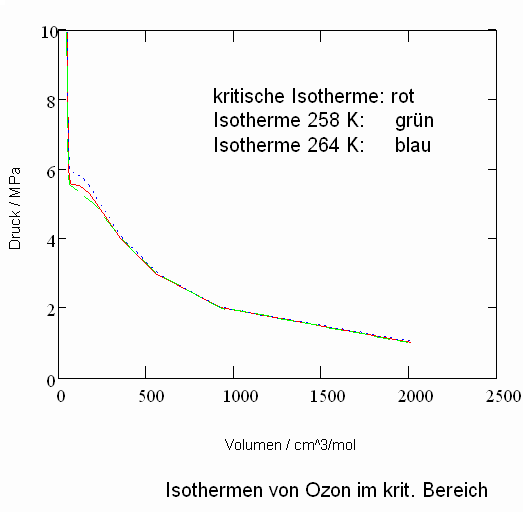
Ein weiteres Beispiel eines wichtigen Stoffes mit nur unvollständigen Angaben in frei verfügbaren Datenbanken ist Ozon O3. Angegeben werden i.a. die kritischen Daten für Temperatur, Druck und Volumen Tk = 261.05 K, pk = 5.46 MPa, vk = 89.38 cm^3/mol. Auch der normale Siedepunkt bei 161.25 K und der Tripelpunkt bei 80.45 K wird genannt.
Allein mit solchen Angaben ist es nun auf der Grundlage der gen. Gesetzmäßigkeiten kritischer Phänomene möglich, pvT- Daten in der kritischen Region und darüber hinaus zu berechnen. Für Ozon z. B. ergeben sich so die folgenden Diagramme für Isothermen in der kritischen Region.
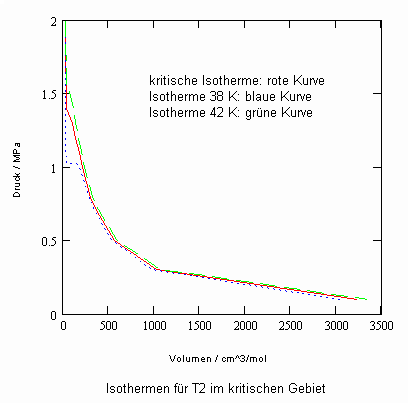
Ein anderes interessantes Beispiel zur Erfassung von pvT-Daten in der kritischen Region ist Tritium T2. Das Molekül besteht aus zwei Tritium- Atomen, wobei der Tritiumkern selbst aus zwei Protonen und einem Neutron besteht. Die folgenden Daten werden in internationalen Datenbanken genannt: Tk = 40.55 K, vk = 57.0576. Der normale Siedepunkt wird mit 25.03 K angegeben.
Für Tritium T2 können als Näherung die folgenden pvT- Daten in der kritischen Region entsprechend folgenden Diagramms berechnet werden:
Für viele weitere Stoffe können nun was hier gezeigt werden sollte- bei bekannten kritischen Daten näherungsweise pvT- Angaben für das kritische Gebiet und auch weit darunter bzw. darüber berechnet werden!
Zur Genauigkeit der Berechnung von pvT- Daten in der kritischen Region
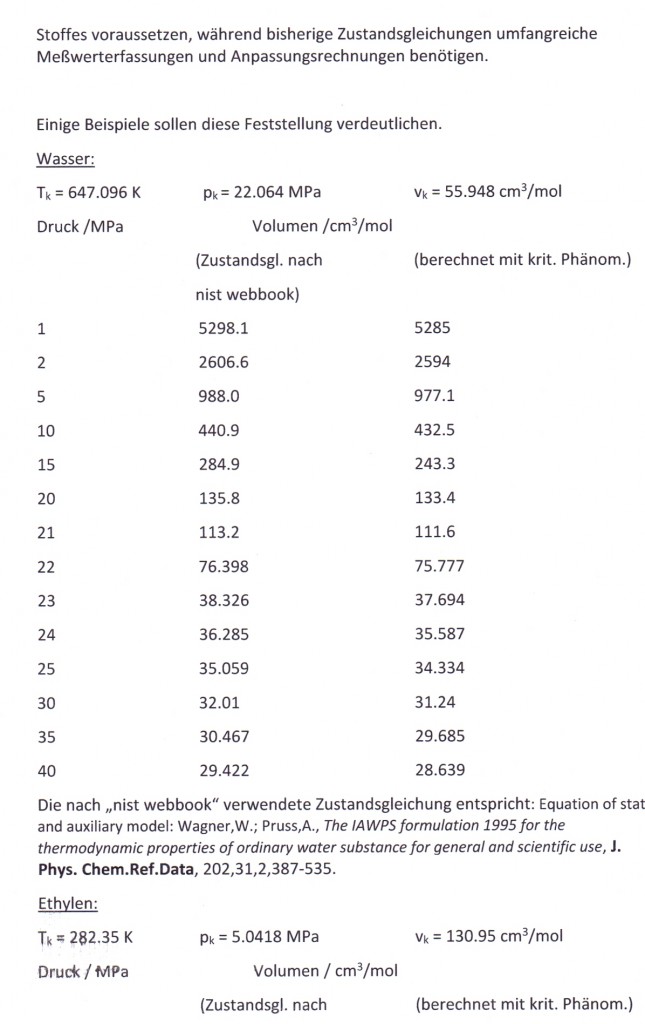
April 15th, 2013Für technisch wichtige Stoffe existieren heute recht genaue Zustandsgleichungen, die die Variablen Druck p, Temperatur T und Volumen v bzw. die Dichte ρ sowohl im Flüssigkeits- als auch im Gaszustand miteinander verbinden. Da es für die in der verfahrenstechnisch – großtechnischen Praxis bestehenden Anforderungen auf eine hohe Genauigkeit ankommt, reichen Berechnungsgleichungen auf Modellvorstellungen der Theoretischen Physik (auf der Basis der van der Waals- Gleichung und ihren vielen sogen. halbempirischen Weiterentwicklungen, der Virialgleichung usw. bis hin zur sogen. molekularen Thermodynamik) nicht aus. Deshalb müssen immer noch Zustandsgleichungen mit ausgeprägt empirischen und stoffspezifischen Anteilen verwendet werden, um die erforderliche Genauigkeit zu ermöglichen. Der Aufwand ist hoch. Er setzt sehr genaue und umfangreiche pvT- Messungen des jeweiligen Stoffes voraus, um die erforderlichen Anpassungen der experimentell ermittelten Zustandsdaten an Parameter vorausgesetzter Zustandsgleichungen zu ermöglichen. Die Erfolge dieser Vorgehensweise mit weitgehend empirischen und „halbempirischen“ Zustandsgleichungen sind offensichtlich.
Selbst für den die menschliche Existenz begründenden Stoff „Wasser“ sind solch weitgehend empirische Zusammenhänge auf der Grundlage sehr genauer pvT- Messungen entwickelt worden (entsprechend der sogen. IAPWS formulation- „International Association for the Properties of Water and Steam“), keineswegs aber auf der alleinigen Grundlage eines nur physikalisch begründeten Modells. Auch für die wichtigen Stoffe der Erdöl- und Erdgasgewinnung und Verarbeitung- wie z.B. Methan, Ethan……bis Benzol, Toluol usw.- existieren Zustandsgleichungen dieser Art.
Meßwerte vieler Substanzen sind heute in Datenbanken dokumentiert, die einen schnellen Zugriff (allerdings oft gebührenpflichtig) über das Internet gestatten (s. z.B. die umfangreiche Stoffdatensammlung „dechema.de/detherm“). Die Bereitstellung von Stoffdaten geht unterdessen so weit, für eine Vielzahl technisch wichtiger Stoffe komplette pvT-Datensätze und auch kalorische Daten anzugeben (s. „nist webbook“), die nach Vorgabe von Druck und Temperatur entsprechend der jeweiligen Dichte bzw. des Volumens mit einer weitgehend an Meßwerte angepaßten Zustandsgleichung ermittelt wurden- und das sowohl für die flüssige Phase und auch für die Gasphase und überkritische Zustände. Die Fehler dabei sind durchaus gering und liegen oft nur im Prozentbereich oder sogar darunter. Sie sind so geeignet für verfahrenstechnische Auslegungen großtechnischer Prozesse mit solchen Stoffen.
Dies alles trifft zu nur für pvT- Zustände weiter entfernt von den kritischen Daten. Soll bei Vorgabe von Druck und Temperatur in einem nahkritischen Bereich die Dichte bzw. das Volumen eines Stoffes mit einer solchen Zustandsgleichung bestimmt werden (dokumentiert z.B. in „nist webbook“) ist das zwar möglich- die Fehler aber werden dann oft als „höher“ im Vergleich zu den Fehlern angegeben, die in Zuständen weiter entfernt von den kritischen Daten festgestellt sind. So heißt es dann z.B. bei nist webbook für Ammoniak: „The uncertainties of the equation of state are o.2% in density….., except in the critical region“.
Und so etwa lauten ähnliche Feststellungen für auch ander Stoffe:
– „Uncertainties will be higher near the critical point“- nist webbook für H2S
– „In the critical region the uncertainties are higher for all properties, except vapor pressure“- nist webbook für SO2.
Die Liste von Stoffen mit der Aussage „except in the critical region“ zu den in der Literatur angegebenen Zustandsgleichungen kann fortgesetzt werden, z. B. mit solchen grundlegenden und strukturell einfachen Stoffen wie Pentan, Propylen, Methan u.a. So ist also die Feststellung gerechtfertigt, dass die Ungenauigkeiten bisheriger veröffentlichter Zustandsgleichungen speziell in der kritischen Region selbst nach den durchgeführten sehr genauen pvT-Messungen und Anpassungen immer noch recht hoch sind. Der Aufwand ist hoch in Relation zum Ergebnis.
Die Hoffnung, dass sich mit den von der Theoretischen Physik festgestellten Gesetzmäßigkeiten kritischer Phänomene akzeptable Berechnungsgleichungen ohne empirische Anteile ergeben könnten, die zwar nicht der klassischen van der Waals- Thermodynamik und den daraus resultierenden Gleichungen bis hin zur sogen. molekularen Thermodynamik entsprechen, aber doch ausreichenden Genauigkeitsansprüchen genügen, hat sich seit Jahren nicht erfüllt.
Nun hat es sich aus theoretischen Erwägungen zur Physik kritischer Phänomene ergeben, einen anderen als bisherige Ansätze zur Auswertung dieser Phänomene zu verfolgen.
Das bisherige Theorie- Ergebnis ist, dass man bei Kenntnis nur der kritischen Daten eines Stoffes weitgehend zutreffende Näherungsaussagen zum pvT- Verlauf der kritischen Isotherme bzw. von nahkritischen Isothermen erhalten kann- ohne zusätzliche Meßwerte. Für Stoffe also, zu denen keine weiteren Messungen außer denen der kritischen Daten vorliegen, können dann zumindest Näherungen des Isothermen -Verlaufs in der kritischen Region abgeleitet werden. Da das für sehr, sehr viele Stoffe zutrifft, ist es also durchaus möglich, die Daten der kritischen Isotherme und auch pv-Daten etwas unterhalb und oberhalb der kritischen Temperatur als Näherung zu berechnen. Nähere Ausführungen zur Theorie und zu Beispielrechnungen sind im Artikel vom 1.7.12 in www.dr-tampe.de u.a. enthalten.
Bisher war es nicht möglich, die Sättigungsvolumina der siedenden Flüssigkeit und des Sattdampfes für Temperaturen kurz unter der kritischen Temperatur vorauszuberechnen. Mit den neuen Theorie- Ergebnissen zu kritischen Phänomenen erweist sich das unterdessen als möglich. Die berechneten Volumina sind Näherungen, die durchaus weitgehend mit Meßwerten übereinstimmen (s. Artikel“ Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur“ in www.dr-tampe.de .)
Die Anwendbarkeit kritischer Phänomene zur Berechnung von pvT- Daten
Februar 23rd, 2013Die für Stoffeigenschaften maßgeblichen Wechselwirkungen zwischen den Molekülen und Atomen eines Stoffes haben eine Reichweite von nur einigen Molekül- bzw. Atomdurchmessern. Im kritischen Zustand und in seiner Nähe entsteht allerdings ein universelles Verhalten physikalischer Größen wegen des Eintretens sogen. „kritischer Fluktuationen“, die sich wie eine beträchtliche Vergrößerung der sogen. Korrelationslänge auswirken. Es entstehen kritische Phänomene. Dies hat zur Folge, daß Eigenschaften völlig unterschiedlicher Stoffe sich im nahkritischen Zustand nach analog gleichen Gesetzmäßigkeiten verhalten, so als ob individuelle Stoffeigenschaften verschwinden.
Kritische Phänomene sind z. B. erklärt für
– den Dichtesprung zwischen flüssiger und dampfförmiger Phase
– die Differenz vom Druck zum kritischen Druck bzw. von der Dichte zur kritischen Dichte auf der kritischen Isotherme
– Kompressibilitäten
-Wärmekapazitäten
– magnetische Zustände (Suszepilitäten) bei verschwindendem Feld.
Die Aussagen der klassischen Theorien treffen für nahkritische Zustände realer Gase und Flüssigkeiten nicht zu.
Die heutigen thermischen Zustandsgleichungen als Grundlage der Berechnung von Stoffdaten für Flüssigkeiten und Gasen beruhen alle letzlich auf der physikalisch begründeten van der Waals- Gleichung , der Virialgleichung, auf Ansätzen der Statistischen Thermodynamik und vor allem immer wieder auf Parameter – Anpassungen empirischer Berechnungsgleichungen an Meßwerte. Der Aufwand ist hoch. Die empirische Vielfalt ist kaum noch überschaubar. Sie ist mit hohem Aufwand zur Bestimmung der Meßwerte verbunden. Die unter Physikern manchmal ironisch geäußerte Kritik, daß die sogen. „halbempirischen Zustandsgleichungen“ und andere rein empirische Gleichungen (z. B. die für nahkritische Zustände ) ja höchstens ein empirisch erforderliches Niveau von wenigstens nur zur Hälfte oder weniger erfüllen, charakterisiert die Situation.
Die Theoretische Physik muß trotz der unzweifelbaren verfahrenstechnischen Empirie- Erfolge der letzten Jahrzehnte Richtschnur im Labyrinth der Möglichkeiten bleiben. Die Suche nach physikalisch begründeten neuen Ansätzen mit geringen empirischen Anteilen sollte gerade auf dem Gebiet der Berechnung von Druck p, Volumen v, Temperatur T- Daten aktuell sein und bleiben.
Die Theoretische Physik formuliert eine sogenannte Universilatitätshypothese: „Die kritischen Exponenten sind fast universell, d. h. für alle thermodynamischen Systeme gleich.“ (s. Nolting: Grundkurs Theoretische Physik, Statistische Physik, Springer Verlag 2004), (R.B. Griffiths: Phys. Rev.Lett.24, 1949 (1970)). Diese Hypothese wird unterdessen als bewiesen betrachtet (Renormierungsgruppentheorie von K. Wilson).
Entsprechend der Universalitätshypothese haben also z. B. die kritischen Exponenten β und δ der kritischen Phänomene – Dichtesprung und Druck- bzw. Dichtedifferenz auf der kritischen Isotherme für völlig verschiedene Stoffe die jeweils fast gleichen Werte. Diese sehr erstaunliche Eigenschaft wird als Folge einer beträchtlichen Vergrößerung der Korrelationslänge von Teilchenwechselwirkungen in der Nähe des kritischen Punktes erklärt.
Im Ergebnis der für den Dichtesprung und die kritische Isotherme durchgeführten Untersuchungen erweist es sich als möglich, wesentliche Schlußfolgerungen zum Verhalten realer Gase und Flüssigkeiten in der Umgebung des kritischen Punktes und auch für Zustände weit unter der kritischen Temperatur abzuleiten.
Und hier ist das theoretische Problem.
Die Gesetzmäßigkeiten kritischer Phänomene sind nur erklärt in einem engem Intervall von Zustandsdaten um den kritischen Punkt. Die Erweiterung des Gültigkeitsbereichs von Gesetzmäßigkeiten kritischer Phänomene weiter entfernt vom kritischen Punkt, also nicht nur für Zustände in unmittelbarer Nähe des kritischen Punktes, dürfte deshalb unmöglich sein. Aber das ist nicht der Fall. Denn es zeigt sich bei der Auswertung von Meßdaten an den verschiedensten Stoffen, daß es möglich ist, Gesetzmäßigkeiten kritischer Phänomene zur Bestimmung von Zustandsdaten auch weit entfernt von der kritischen Temperatur und vom kritischen Druck anzuwenden. Die Ergebnisse stimmen dann durchaus mit Meßwerten überein.
In Auswertung solcher Ergebnisse der Untersuchung von Stoffwerten wurde als Hypothese die Erweiterbarkeit der Gesetzmäßigkeiten kritischer Phänomene auf Zustände weiter entfernt vom kritischen Punkt vorausgesetzt. Durch die vorliegenden Ergebnisse mit Untersuchungen an konkreten Stoffdaten ist diese Hypothese als berechtigt dargestellt.
Die physikalische Begründung allerdings fehlt.
Das Anliegen dieser Schrift ist es, theoretische Physiker und Theoretiker der physikalischen Chemie und auch theoretische Kenntnisse besitzende Verfahrenstechniker zu veranlassen, die Gründe der Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene weit über nahkritische Verhältnisse hinaus zu suchen und zu benennen.
Ergebnisse bisheriger Untersuchungen auf der Grundlage der o.gen. Hypothese sind die folgenden.
Für reale Gase niedriger bis hoher Drücke ergibt sich auf der gen. Grundlage ein funktionaler Zusammenhang zwischen dem Druck p und dem molaren Volumen v auf einer Isotherme der Temperatur T entsprechend der Gleichung
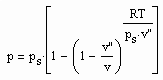, (I)
wobei ps der Dampfdruck, v“ das molare Sättigungsdampfvolumen und R die allgemeine Gaskonstante ist.
Es zeigt sich weiter, das es mit den auf der Grundlage der Theorie kritischer Phänomene gewonnenen Ergebnisse möglich ist, eine allgemeine Beziehung abzuleiten, die die Berechnung des molaren Volumens v“ trocken gesättigten Dampfes bei bekanntem Dampfdruck ps als grobe Näherung gestattet:
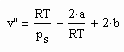. (II)
Dabei sind a und b die Parameter der klassischen van der Waals- Gleichung realer Gase, die nur von den kritischen Daten Tk (kritische Temperatur) und pk (kritischer Druck) abhängen. Die sinnvolle Anwendung dieser Gleichung ist für Zustände näherungsweise von niedrigen bis hohen Temperaturen gegeben, nicht aber für nahkritische Verhältnisse.
In Auswertung der zu kritischen Phänomenen durchgeführten Untersuchungen ergab sich weiterhin die Gleichung
, (III)
die von niedrigen bis zu hohen Temperaturen gilt. Dabei ist der kritische Exponent β mit dem Wert 1/3 vorausgesetzt. Kv ist die sogen. Dichtesprungkonstante, die einfach berechnet werden kann. Die obige Gleichung (III), die dem Dichtesprung zwischen siedender Flüssigkeit des Volumens v‘ und dem Sattdampfvolumen v“ entspricht, ermöglicht die Berechnung des Sättigungsvolumens v‘ der Flüssigkeit bei gegebener Temperatur, wenn v“ bereits mit (II) berechnet werden konnte. Für das Siedevolumen der Flüssigkeit ergibt sich näherungsweise
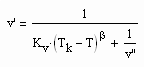. (IV)
Damit sind bei vorgegebener Temperatur und bekanntem Dampfdruck die Sättigungsvolumina v‘ und v“ eines Stoffes näherungsweise berechenbar, wenn die kritischen Daten bekannt sind.
Für Zustände kurz unter der kritischen Temperatur bestehen wegen der am kritischen Punkt sich beträchtlich vergrößernden Fluktuationen veränderte Bedingungen, die zu anderen sich aus (III) ableitbaren Berechnungsgleichungen führen. Damit sind dann sogar die Sättigungsvolumina v‘ und v“ und auch der Dampfdruck ps für Temperaturen kurz unter der kritischen Temperatur als Näherungen berechenbar.
Speziell für Flüssigkeiten in nahkritischen und auch bis weit unterkritischen Zuständen kann eine Zustandsfunktion abgeleitet werden, die die Berechnung des jeweiligen Flüssigkeitsvolumens bei vorgegebenem Druck und vorgegebener Temperatur als Näherung gestattet. Damit ist dann das Flüssigkeitsverhalten eines Stoffes für das gesamte Existenzgebiet vom Dampfdruck sogar bis zu höheren Drücken im 10 MPa- Bereich und teilweise darüber erfaßt- wie Nachrechnungen an gut vermessenen Stoffbeispielen zeigen.
Alle bisherigen Ansätze zu einer allgemeinen Theorie der Flüssigkeiten gehen letztlich vom jeweiligen Molekülaufbau, von den zwischenmolekularen Wechselwirkungen, von molekulartheoretischen Ansätzen der Quantenmechanik und Statistischen Thermodynamik bis hin zur Statistik mit Monte-Carlo- Modellen usw. aus. Die gesuchte Aussage zu einer möglichst allgemeingültigen Erklärung und mathematischen Fassung der pvT- Eigenschaften von Flüssigkeiten wurde so bisher nicht gefunden.
Für die bei der Auswertung kritischer Phänomene gefundene allgemeine Zustandsfunktion von Flüssigkeiten ist als Ausgangspunkt zur Beschreibung und Erklärung des Verhaltens von Flüssigkeiten nur der kritische Punkt eines Stoffes mit seinen kritischen Phänomenen erklärt, indem die sonst nur in einem engen Bereich um die kritische Temperatur gültigen Gesetze kritischer Phänomene auf Temperaturen weit unterhalb der kritischen Temperatur übertragen werden. Die physikalische Erklärung dazu fehlt!
Mitteilung zu Zustandsgleichungen für reale Gase und Flüssigkeiten- abgeleitet aus der Theorie kritischer Phänomene
November 16th, 2012Für reale Gase wurde mit Gesetzmäßigkeiten kritischer Phänomene die Funktion
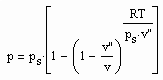(1)
formuliert. Dabei ist p der Druck/MPa, ps der Dampfdruck/MPa, T die absolute Temperatur/K, v das Volumen/cm³/mol, v“ das Sättigungsdampfvolumen cm³/mol und R die allgemeine Gaskonstante 8.314 J/mol K. Die Funktion (1) ergibt sich allein nur mit Kenntnissen über kritische Phänomene ohne Voraussetzung und Anwendung von physikalischen Theorien, die die Anwendung der van der Waals-Thermodynamik und ihren empirischen Weiterentwicklungen, der physikalisch begründeten Virialgleichung und ihren Weiterentwicklungen oder gar der sogen. molekularen Thermodynamik und damit auch deren Vorstellungen über den Molekülaufbau des jeweiligen Stoffes und der molekularen Wechselwirkungen voraussetzen. Die Grundlage dieser Funktion ist nicht die bisherige Thermodynamik, sondern allein nur ein thermodynamisches Modell begründet mit kritischen Phänomenen.
Für Gase besteht neben der physikalisch begründeten van der Waals- Gleichung die ebenfalls physikalisch begründete Virial-Gleichung . Grundlage der Virialgleichung ist die Taylor- Entwicklung des Realgasfaktors Z=pv/RT in eine Reihe für die Dichte 1/v→0. Als Reihenentwicklung wird
Z=1+B/v+C/v²+…… (2)
erhalten. Die Koeffizienten B,C,….werden als 2., 3. usw. Virialkoeffizient bezeichnet. Sie sind nur temperaturabhängig.
Die Berechnung von Zustandsdaten realer Gase gelingt mit der Virialgleichung als Näherung, wenn zumindest der 2. und evtl. 3. Virialkoeffizient bekannt ist. Man sagt, die Funktion Z= 1+B/v ist als Näherung ausreichend bis zu Gasdichten von ca. 0.5 ρk, die Funktion Z= 1+B/v+C/v² bis zu Dichten von ca. o.75 ρk (ρk- kritische Dichte).
Die der o.gen. Funktion (1) entsprechenden Virialkoeffizienten können berechnet werden. Die Kenntnis des 2. Virialkoeffizienten z. B. ist aus folgenden Gründen sinnvoll: Der 2. Virialkoeffizient eines Stoffes nämlich steht mit dem Wechselwirkungspotential der zwischenmolekularen Kräfte zweier Moleküle eines Stoffes in Verbindung. Wenn man den 2. Virialkoeffizienten kennt, muß es der Theoretischen Physik möglich sein, Aussagen zu der wichtigen Potentialfunktion der zwischenmolekularen Kräfte eines Stoffes abzuleiten. Die Statistische Thermodynamik formuliert für den 2. Virialkoeffizienten
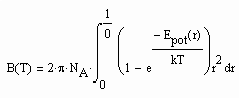. (3)
Dabei ist NA die Avogadrosche Konstante, Epot ist das Potential der zwischenmolekularen Kräfte, k ist die Boltzmann- Konstante und r ist der radiale Abstand zweier Moleküle des jeweiligen Stoffes. Wenn also der Virialkoeffizient B(T) bekannt ist, können Aussagen zu dem molekulartheoretischen sehr grundlegenden Potentialverlauf Epot(r) getroffen werden. Und wenn das möglich ist, ist letzlich auch eine Aussage zum Potentialverlauf zwischenmolekularer Kräfte verschiedener Stoffe möglich, so daß damit dann Gemischeigenschaften erfaßt werden können. Die hierzu erforderlichen weiteren Untersuchungen können hier allerdings nicht dargelegt werden.
Der zur näheren Bestimmung des Potentials zwischenmolekularer Kräfte erforderliche 2. Virialkoeffizient, der sich entsprechend (1) und (2) ergibt, lautet
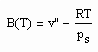. (4)
Am Beispiel Wasser soll gezeigt werden, daß der nach (4) berechnete 2. Virialkoeffizient durchaus dem nach Meßwerten entspricht.
Mit Hilfe der o.gen. Taylor- Entwicklung ist ersichtlich, daß für über alle Grenzen wachsendes Volumen
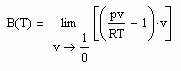(5)
gilt (s. z.B. J. Gmehling, B. Kolbe: Thermodynamik, VCH, 1992). Damit besteht auf einer Isothermen die Beziehung
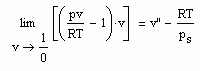
(6).
Das ist aus folgendem Grund interessant: Der Grenzwert auf der linken Gleichungsseite wird experimentell bestimmt, indem bei T=konstant bei vorgegebenem Druck für p gegen O das jeweils zugehörige Volumen gemessen wird. Dies sind dann alles Stoffdaten ohne Bezug zu den Sättigungsdaten v“ und ps. Und trotzdem besteht laut der obigen Gleichung ein Zusammenhang mit dem Sättigungsvolumen v“ und dem Dampfdruck ps! Eine Information zu v“ und ps ist also in dem o.gen. bei verschwindenden Druck experimentell bestimmbaren Grenzwert bereits enthalten.
So wie es möglich war, für reale Gase die Zustandsfunktion (1) entsprechend Gesetzmäßigkeiten kritischer Phänomene abzuleiten, zeigt es sich, daß auch für Flüssigkeiten eine druckexplizite allgemeine Zustandsfunktion ebenfalls nur auf der Grundlage kritischer Phänomene in der Form p = p(v,T) als Näherung bestimmt werden kann. Kenntnisse zum Molekülaufbau und zu Wechselwirkungen innerhalb der Moleküle und zwischen den Molekülen des Materials sind dabei erstaunlicherweise gar nicht erforderlich. Allerdings sind die kritischen Daten pk, vk, Tk und das Flüssigkeitssättigungsvolumen v‘ als bekannte Parameter vorauszusetzen. Die Ableitung der gen. Zustandsfunktionen für reale Gase und für Flüssigkeiten durch Auswertung von Gesetzmäßigkeiten kritischer Phänomene soll mit einer entsprechenden Veröffentlichung 2013 gezeigt werden.