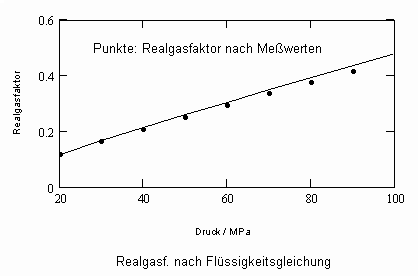
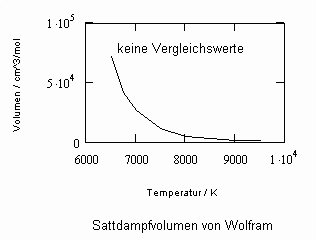
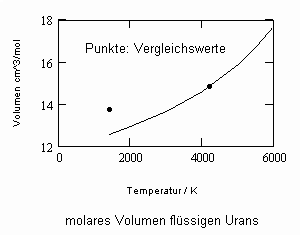
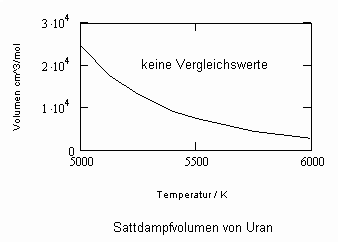
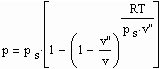Dr. F. Tampe

Zur Berechnung nahkritischer Stoffdaten von Flüssigkeiten und Gasen

Juli 1st, 2012

Aus der physikalischen Theorie kritischer Phänomene kann für reale Gase die Zustandsfunktion

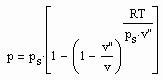(1)

für Zustände entfernt vom kritischen Punkt bzw. für kleine bis mäßige Drücke abgeleitet werden (p- Druck/ MPa, ps- Dampfdruck/ MPa, T- Temperatur / K, v- molares Volumen / cm³/mol, v“- molares Sattdampfvolumen / cm³/mol ). Die Funktion (1) ist als grobe Näherung anwendbar. Sie ist anwendbar auch für hohe Temperaturen, sogar bis über die kritische Temperatur hinaus. Ihre Anwendbarkeit für Zustände nahe des kritischen Punktes ( einige Kelvin unterhalb und oberhalb der kritischen Temperatur Tk und für Drücke in der Nähe des kritischen Druckes pk ) ist nicht zu erwarten, da hier besondere und andere Bedingungen gelten, die sich aus Gesetzmäßigkeiten kritischer Phänomene im Unterschied zur bisherigen van der Waals- Thermodynamik ergeben.

Auf der kritischen Isotherme können entsprechend der Gesetzmäßigkeiten kritischer Phänomene nahe des kritischen Druckes die Relationen

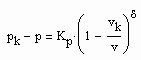(2)

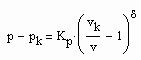(3)

vorausgesetzt werden. Dabei ist Kp ein Proportionalitätsfaktor und δ der entsprechende kritische Exponent. (2) gilt für p ‹ pk , (3) gilt für p › pk.

Für p,v – Zustände nahe pk, vk ist (2), (3) zwingend mit einem in der Theorie kritischer Phänomene erklärten kritischen Exponenten zu rechnen. Der kritische Exponent δ ist resultierend aus Messungen in der Größenordnung von 4.0 bis 4.8 festgestellt worden (s. z. B. Nolting, W.: Statistische Physik, Springer Verlag 2004). Es gibt Physiker, die kritische Exponenten im Sinne absoluter Naturkonstanten unabhängig vom Stoff interpretieren und andere, die eine Stoffabhängigkeit in Grenzen zugestehen. Setzt man die weitgehende Stoffunabhängigkeit voraus, verbleibt der Proportionalitätsfaktor Kp als Unbekannte. Es besteht die Frage, wie ist der Proportionalitätsfaktor Kp zu bestimmen, um Zustände auf der kritischen Isotherme berechnen zu können?

Sinnvoll ist es, die Frage allgemeiner zu stellen. Nämlich: Wie können nahkritische Zustandsdaten mit ausreichender Genauigkeit nicht nur für Zustände auf der kritischen Isotherme, sondern auch für Temperaturen kurz unter- und oberhalb der kritischen Temperatur bestimmt werden? Bisherige physikalisch begründete als auch die sogen. halbempirischen Zustandsgleichungen u.a. reichen nicht aus. Auch die von der bisherigen Theoretischen Physik erklärten Ansätze, die die rechnerische Bestimmung des Proportionalitätsfaktors Kp ohne Meßwerte kaum erlauben, reichen nicht aus. Für technisch wichtige Stoffe ist deshalb die Physikalische Chemie und Verfahrenstechnik auf empirische stoffspezifische Lösungen bei einem hohen meßtechnischen Aufwand angewiesen (vielparametrige empirische Zustandsgleichungen pro Stoff bei Voraussetzung hochgenauer Stoffwerte) ( s. z. B. die Stoffdaten für Erdgaskomponenten, für Kohlenstoffdioxid CO2, für Wasser usw. mit weitgehend empirischen Zustandsgleichungen von Wagner und Span, Universität Bochum, s. E.W. Lemmon u. R. Span: Multiparameter Equations of State for Pur Fluids and Mixtures. Chapter 12, in A.R.H. Goodwin, J.V. Sengers und C.Peters(Ed.): Applied Thermodynamics of Fluids. International Union of Pure and Applied Chemistry, Royal Society of Chemistry, Thomas Graham House,Cambridge, UK 2010)).

Bisherige Feststellungen und Schätzungen kritischer Exponenten für dreidimensionale physikalische Systeme mit einem Ordnungsparameter in der entsprechenden Universalitätsklasse wurden z. B. in Auswerung des Issing – Modells mit dem kritischen Exponenten β = 0.326 + – 0.002 und δ = 4.80+- 0.02 vorausgesetzt (s. z. B. J.V. Senger: Thermodynic Behavior of Fluids near the critical Points, Ann. Rev. Phys.Chem. 1986,37).

Vorliegende Ergebnisse zu Gesetzmäßigkeiten kritischer Phänomene bestätigen zwar die Existenz des kritischen Exponenten β in der Größenordnung von 1/3, nicht aber die Gültigkeit eines allgemeinen Exponenten δ etwa bei 4.8. Das in der Theoretischen Physik gen. Werteintervall δ = 4.0 bis 4.8 trifft zu und ist nach den vorliegenden Untersuchungen durchaus noch zu klein.

Die nachfolgenden Feststellungen weisen darauf hin, daß es möglich ist, einen physikalisch begründeten und empiriefreien Ansatz zur Nachrechnung nahkritischer Daten ohne zusätzlichen Meßaufwand zu finden.

Bestimmt man für die kritische Isotherme vergleichsweise für verschiedene Stoffe den Exponenten RTk/pk vk in (1), ist festzustellen: Es gibt Stoffe, deren Exponent RTk/pk vk in (1) in dem für den kritischen Exponenten δ erklärten Bereich zwischen 4.0 bis 4.8 liegt. Für Wasser z. B. ergibt sich 4.36, für Ammoniak NH3 4.12. Für solche Stoffe ist die weitgehende Gültigkeit der Funktion (1) auch im nahkritischen Bereich zu erwarten. Die kritische Isotherme sollte in diesen Fällen entsprechend (1) mit

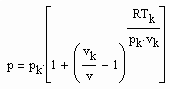v‹ vk (4)

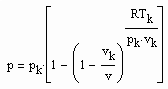v›vk (5)

erfaßt werden können.

Ob das tatsächlich so ist, zeigt die Nachrechnung mit Daten gut vermessener Stoffe wie z. B. für Wasser.

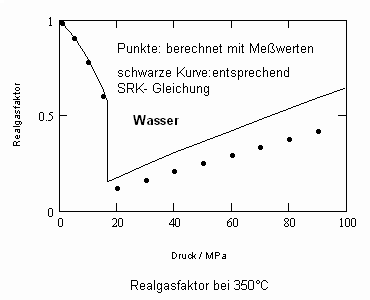
Wasser: (Tk= 647.15 K, pk= 22.055 MPa, vk= 55.9503 cm³/mol)

Bei einer Temperatur 648.15 K (375 °C, also 1°C über der kritischen Temperatur) und einem hypothetischen Dampfdruck von 22.286 MPa ergeben sich mit den o. gen. Funktionen (4), (5) im Vergleich mit aus Meßwerten berechneten Realgasfaktoren die folgenden Werte (außerdem sind die Werte angegeben, die sich mit einer der oft angewendeten Ingenieurgleichungen, der Soave- Redlich- Kwong- Gleichung berechnen lassen).

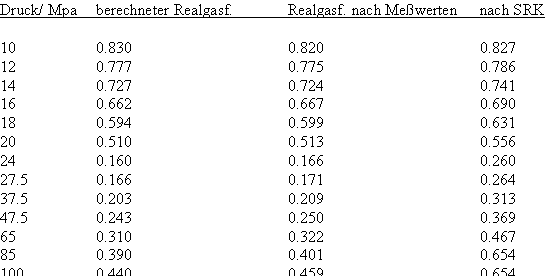
(Meßwerte L. Haar, J.S. Gallagher, G.S. Kell: NBS/NRC Wasserdampftafeln, Springer 1988)

Ein weiteres für die kritische Isotherme vermessenes und veröffentlichtes Beispiel ist

Schwefelhexafluorid SF6: (Tk= 318.7232 K, pk= 3.755 MPa, vk= 196.576 cm³/mol)

Bei einer Temperatur genau auf der kritischen Isotherme ergeben sich mit den o.gen. Funktionen (4), (5) im Vergleich mit aus Meßwerten berechneten Realgasfaktoren die folgenden Werte:

Die gen. Beispiele u.a. zeigen die Anwendbarkeit der Funktionen (4), (5) für kritische Verhältnisse.

Für Stoffe allerdings, deren Exponent RTk/ pk vk nicht in das von der physikalischen Theorie erklärte Wertebereich von ca. 4.0 bis 4.8 für kritische Exponenten fällt, bestehen andere Bedingungen. Allerdings ergibt sich auch für solche Stoffe die Möglichkeit, nahkritische Stoffdaten rechnerisch zu bestimmen. Es ist dazu nur die Kenntnis der kritischen Daten und die vorausgesetzte Temperatur ohne weitere Meßwerte erforderlich.

Die so feststellbare Zustandsfunktion p = p(T,v) gestattet dann auch die Berechnung kalorischer Größen- wie auch der wichtigen Freien Enthalpie für nahkritische Zustände.

Die vorliegenden Theorie – Ergebnisse sollen veröffentlicht werden.

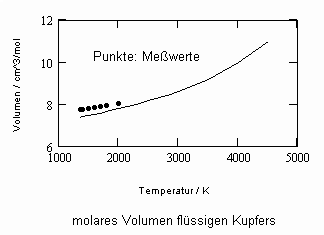
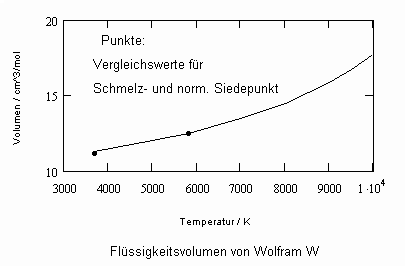
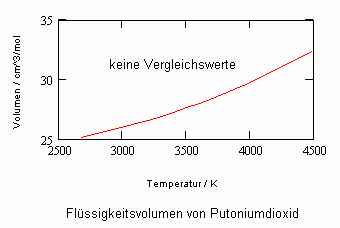
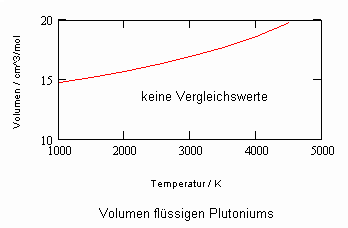
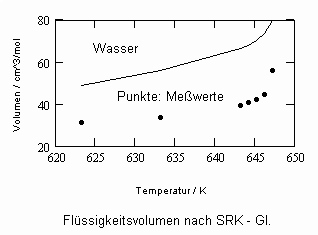
Die sich aus der Theorie kritischer Phänomene ergebenden Weiterentwicklungen ermöglichen es, allgemeine Aussagen zum pvT- Verhalten von Flüssigkeiten abzuleiten. Es ergibt sich eine Zustandsfunktion speziell für Flüssigkeitenvon niedrigen Temperaturen bis hin zu Temperaturen nahe der kritischen Temperatur. Damit kann bei vorgegebener Temperatur und vorgegebenem Druck das molare Volumen einer Flüssigkeit als Näherung selbst bis zu hohen Drücken von einigen 10 MPa und höher berechnet werden, wenn nur die kritischen und die Sättigungsdaten des jeweiligen Stoffes bekannt sind. Die Berechnung der Realgasfaktoren von Flüssigkeiten bis zu hohen Drücken ist somit bei guter Übereinstimmung mit Meßwerten möglich.

Für Flüssigkeitszustände bei Temperaturen niedriger bis mäßiger Dampfdrücke, d.h. weiter entfernt vom kritischen Punkt des jeweiligen Stoffes, ist mit den Mitteln der van der Waals- Thermodynamik die Zustandsfunktion

(6)

ableitbar (b- Eigenvolumen der Moleküle des Stoffes/ cm³/mol, K-stoffspezifische Konstante mit der Dimension eines Druckes, die sich aus dem Dampfdruck ergibt) (s. Tampe,F.: Stoffwerte von Flüssigkeiten und Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene, 2009, ISBN 978-3-00-027253-0).Auch diese Funktion ermöglicht die Berechnung der Flüssigkeitsvolumina als Näherung für Drücke vom Dampfdruck bis weit darüber hinaus- z.B. für Wasser sogar bis 100 MPa. Mit dieser Funktion (6) und der aus der physikalischen Theorie kritischer Phänomene ableitbaren Zustandsfunktion für Flüssigkeiten nahe kritischer Werte ist die Berechnung von Flüssigkeitsdaten als Näherung in ihrem gesamten Existenzbereich von niedrigen bis zu hohen Temperaturen, vom Dampfdruck bis zu hohen Drücken möglich.

Die in der Technischen Thermodynamik , Physikalischen Chemie und Verfahrenstechnik bestehenden Ansätze, Stoffeigenschaften mit den Mitteln der bisherigen van der Waals- Thermodynamik, der Statistischen Thermodynamik mit Mitteln von Potential- Ansätzen der Quantenmechanik bzw. der sogen. molekularen Modellierung zu bestimmen, erweisen sich oft als kompliziert und empiriebelastet. Als viel einfacher gestalten sich die aus Gesetzmäßigkeiten kritischer Phänomene ableitbaren Berechnungsgleichungen, die nicht einmal Anpassungsrechnungen an vorausgesetzte empirische Parameter verlangen.

Weitere Beispiele zu Rechenergebnissen im Vergleich zu Meßwerten können die Anwendbarkeit der gewonnenen Theorie – Ergebnisse, die Näherungen der entsprechenden Stoffwerte erlauben, verdeutlichen: s. Anlage.

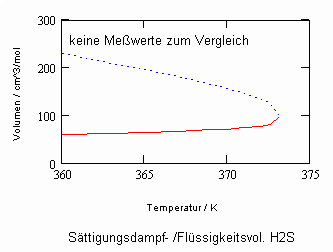
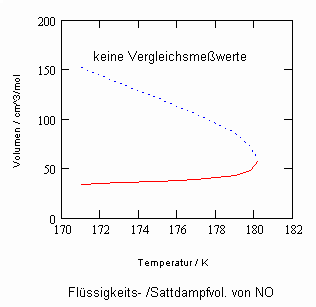
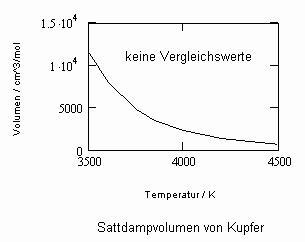
Oftmals sind Meßwerte des nahkritischen Sättigungszustandes von Stoffen unbekannt. Die Berechnung solcher Daten für Flüssigkeits- und Dampfvolumina bzw. für Dampfdrücke in der Nähe der kritischen Temperatur ist mit den gegenwärtig verfügbaren Berechnungsgleichungen (van der Waals- Gleichung, sogen. halbempirische Gleichungen nach Soave, Redlich, Kwong und Peng, Robinson u. a., Gleichungen der Statistischen Thermodynamik usw.) in vielen Fällen nicht möglich bzw. zu ungenau.

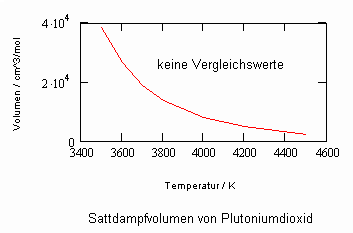
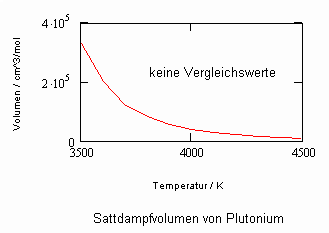
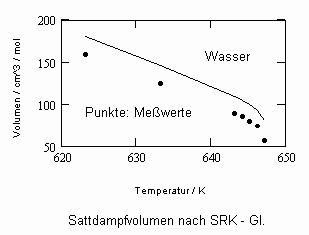
In Auswertung von Gesetzmäßigkeiten kritischer Phänomene ergibt sich nun die Möglichkeit, nahkritische Sättigungsvolumina bzw. die nahkritischen Dichten von Stoffen für Flüssigkeit und Dampf im Sättigungszustand in Abhängigkeit von der Temperatur zu berechnen. Die Berechnungsgleichungen dafür liegen vor. Die Ergebnisse sind Näherungen, die für den Flüssigkeitszustand sogar besser sind als für den Sattdampf (s. auch Artikel „Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur“ vom 22.2.2011 in www.dr-tampe.de )

Auf Folgendes ist hinzuweisen: Wenn die Zustandsfunktion p= p(v,T) eines Stoffes sowohl sowohl für den Flüssigkeits- als auch für den Gaszustand bekannt ist, muß es möglich sein, kalorische Daten dieses Stoffes zu berechnen. Zur Berechnung z.B. der für technische Belange wichtigen Enthalpie gilt

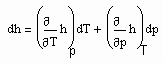. (7)

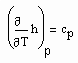(8)

die spezifische Wärmekapazität ist, die gemessen werden kann, und für

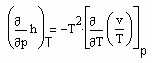(9)

gilt, ist damit die Enthalpie eines Stoffes sowohl für den Flüssigkeitszustand als auch den Gaszustand berechenbar. Dies bedeutet weiter, daß so die Enthalpie eines Stoffes entlang der Dampfdruckkurve sowohl für die Flüssigkeit als auch für den Sattdampf als Näherung berechnet werden kann.

Anlage: Berechnungsbeispiele

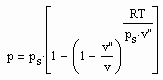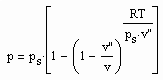
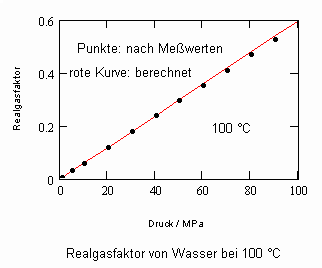
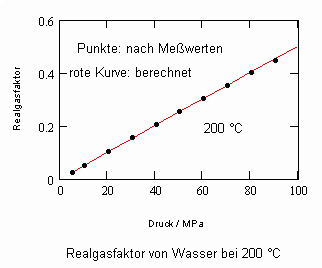
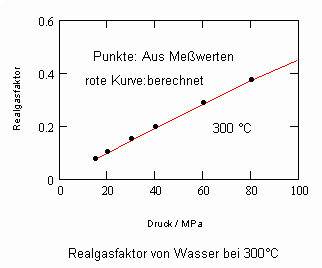
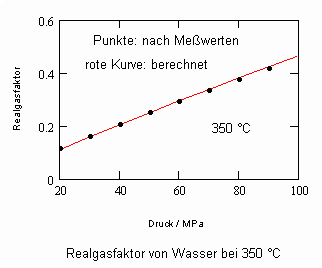
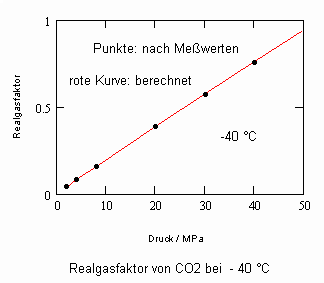
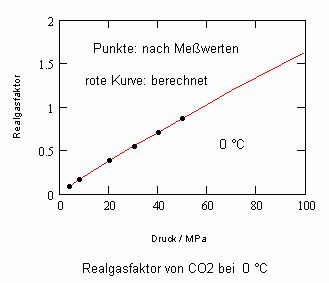
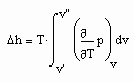
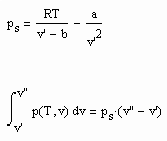
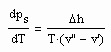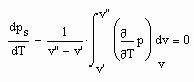
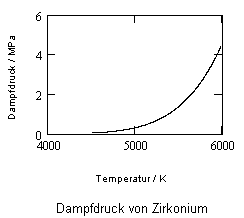
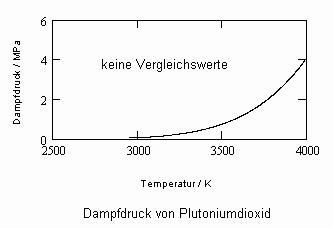
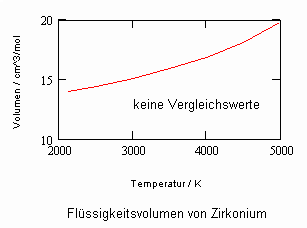
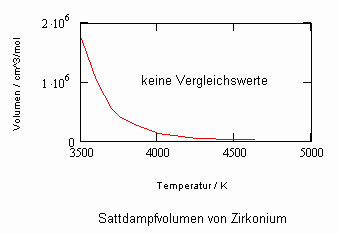
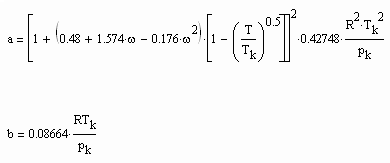
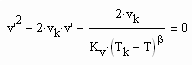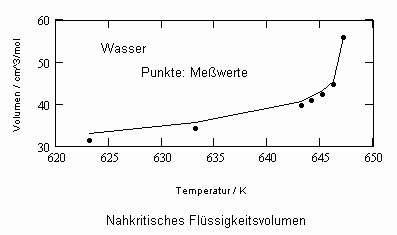
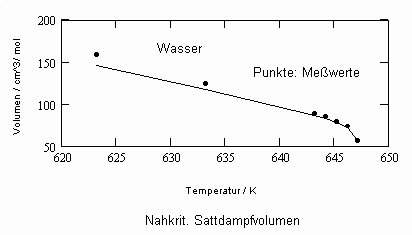
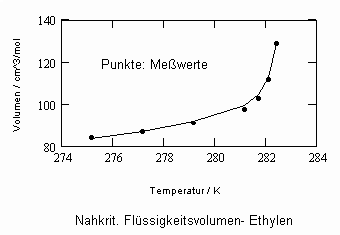
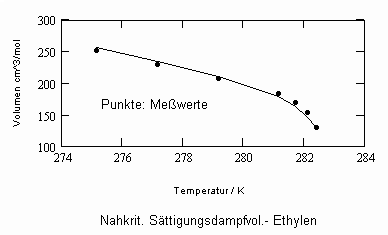
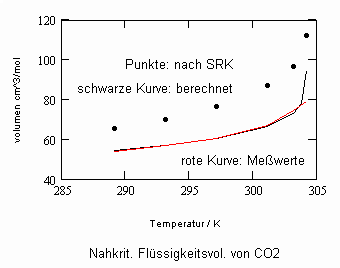
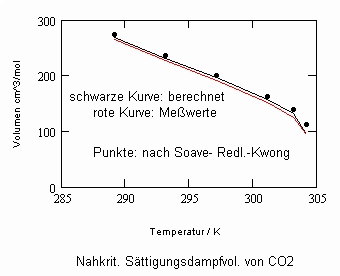
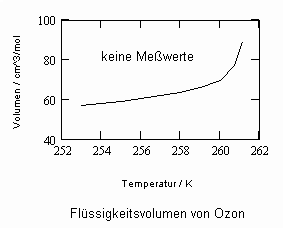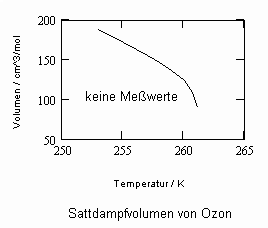Posted in Dichte von Flüssigkeiten und Gasen, nahkritische Stoffdaten von Flüssigkeiten und Gasen, Sättigungsdaten-Flüssigkeiten und Gase, Universalitätshypothese, Zustandsgleichung | Kommentare deaktiviert für Zur Berechnung nahkritischer Stoffdaten von Flüssigkeiten und Gasen

Gedanken zur Universalitätshypothese kritischer Phänomene

Dezember 18th, 2011

Die in diesem Blog gen. und in einzelnen Artikeln beschriebenen neuen Möglichkeiten der Berechnung thermophysikalischer Daten von Flüssigkeiten und Gasen wurden durch eine Erweiterung der für nahkritische Zustände geltenden Gesetze kritischer Phänomene auf vom kritischen Punkt weit entfernte Zustände gewonnen.

Kritische Phänomene sind in einem engen Bereich der Temperatur oder des Drucks nahe der kritischen Daten untersucht und mit ihren kritischen Exponenten erklärt (s. Artikel vom 1.5.2009 „Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene“ und die Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ – ISBN 978-3-00-027253-0) . In der physikalischen Literatur ist die Wirkung kritischer Phänomene auf Zustandsdaten von Stoffen begrenzt auf sehr nahkritische Verhältnisse- bis einige wenige Kelvin der Temperatur T unter bzw. über der kritischen Temperatur Tk oder nur nahe am kritischen Druck pk. So z. B. heißt es: „Man spricht von kritischen Phänomenen. Ihre Universalität erklärt das heftige Interesse an diesen Phänomenen, obwohl sie sich nur im Bereich der kritischen Fluktuationen, also in einem nur sehr schmalen Temperaturbereich abspielen.“ (Nolting: Grundkurs Theoretische Physik 6, Statistische Physik, Springer 2004.)

Mit den vorliegenden Ergebnissen zumindest für die kritischen Phänomene

– Dichtesprung ρ‘-ρ“ zwischen flüssiger und dampfförmiger Phase im Sättigungszustand

– Differenz vom Druck p zum kritischen Druck pk bzw. von der Dichte ρ zur kritischen Dichte ρk auf der kritischen Isotherme Tk

scheint das aber nicht so zu sein!

Denn es zeigt sich, daß die Proportionalitäten zwischen der Dichtedifferenz ρ‘-ρ“ und (Tk-T)^β (für T<Tk) bzw. p-pk und sign(ρ-ρk)(⁄ρk-ρ⁄)^δ keineswegs nur in der unmittelbaren Nähe des kritischen Punktes gelten. Der Beleg dafür ist die Anwendbarkeit der Gleichungen

und

die ja erst durch die Erweiterung der gen. beiden kritischen Phänomene auf weit von der kritischen Temperatur entfernte Temperaturen gewonnen werden konnten (ps- Dampfdruck, Kv- sogen. Dichtesprungfaktor), (s. o. gen. Artikel vom 1.5.2009 ). Die gen. beiden Gleichungen gelten trotz ihrer Ableitung aus Gesetzmäßigkeiten kritischer Phänomene keineswegs nur in der unmittelbaren Nähe des kritischen Punktes eines Stoffes. Sie können- wie in den verschiedenen Artikeln dieses Blogs aufgezeigt- durchaus zur näherungsweisen Berechnung von Stoffdaten benutzt werden. Die physikalische Theorie hierzu und die Ableitung dieser und weiterer Gleichungen ist in der o.gen. Veröffentlichung ausführlich dargelegt.

Entsprechend der Universalitätshypothese von Griffiths (R.B. Griffiths, Phys. Rev. Lett. 24, 1479 (1970)) haben die kritischen Exponenten für völlig verschiedene Stoffe fast die gleichen Werte (s. z. B. Nolting: „Grundkurs Theoretische Physik 6, Statistische Physik“, Springer Verlag 2004). Diese sehr erstaunliche Eigenschaft der verschiedensten Stoffe trifft zu- aber eben doch nur fast!

Theoretische Physiker erklären die Universalitätshypothese als unterdessen bewiesen entsprechend der Renormierungsgruppentheorie von K. Wilson.

Damit ist letztlich gesagt, daß die Universalitätshypothese selbst für Stoffe komplizierter chemischer Strucktur zutreffen muß- also nicht nur für Stoffe einfacher Moleküle (wie N2,O2, Ar, He, H2 usw.), für die die meisten Messungen vorliegen, sondern auch für Stoffe größerer Molekülmasse mit z.B. C- Doppelbindungen, aromatischen Ringen, Heterocyclen und der ungeheuren Vielzahl weiterer anorganischen und organischen Verbindungen.

Die Frage,ob das angesichts der überwältigenden Vielfalt von Stoffen immer so entsprechend der Universalitätshypothese tatsächlich ist ( sie selbst formuliert die Einschränkung „fast“ ), muß wohl erlaubt sein. Denn es ist zu bedenken, daß notwendige Untersuchungen und Messungen mit geringer Fehlertoleranz in der Nähe des kritischen Punktes schwierig sind. Nur für relativ wenige Stoffe liegen z.B. p,v- Messungen auf der kritischen Isotherme vor.

Wenn die Universalitätshypothese von einer nur „fast“ zutreffenden Universalität der kritischen Exponenten spricht, ist offensichtlich eine Variabilität dieser Exponenten im Rahmen der Vielfalt unterschiedlicher Stoffe zugelassen. Es ist zu fragen, ob für diese Variabilität die Ungenauigkeit der schwierigen Messung verantwortlich ist oder ob der jeweilige kritische Exponent doch etwas vom Stoff abhängig ist. Auch Nachfragen dazu bei namhaften theoretischen Physikern konnten diese Frage nicht völlig klären. Teilweise wurde auf immer feste Werte der kritischen Exponenten verwiesen, teilweise wurde die Variabilität bei komplizierteren Molekülen und bei veränderten sogen. Universalitätsklassen benannt.

Keineswegs ist es so, daß die Variabilität kritischer Exponenten nur klein ist. Sehr deutlich zeigt sich das an dem kritischen Phänomen,welches den nahkritischen Zusammenhang von Druck und Dichte auf der kritischen Isotherme beschreibt. Für den dazu in der physikalischen Literatur benannten kritischen Exponenten δ wird immerhin ein beträchtlicher Wertebereich von 4 bis 4.8 genannt. Eine weit geringere Streuung der festgestellten Werte des kritischen Exponenten besteht für das kritische Phänomen, das den nahkritischen Dichteverlauf in Abhängigkeit von der Temperatur mit dem in der physikalischen Literatur bezeichneten Exponenten β beschreibt. Die Werte für β streuen nur von 0.33 bis 0.37. Obwohl der versuchstechnische Nachweis und die Gültigkeit des mit dem kritischen Exponenten β verbundenen kritischen Phänomens der Proportionalität der Dichtedifferenz ρ‘-ρ“ mit der Temperaturdifferenz entsprechend (Tk-T)^β nur für Temperaturen in unmittelbarer Nähe der jeweiligen kritischen Temperatur erklärt ist, ergab sich der Nachweis dafür, daß die gen. Proportionalität auch für Zustände weit entfernt von der kritischen Temperatur gilt. Der Ausdruck dafür ist die bereits o. gen. Gleichung

die die Grundlage wesentlicher Stoffdatenberechnungen der Artikel dieses Blogs und der Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen – berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0) ist. Wirklich interessant ist, daß diese Gleichung , obwohl sie eigentlich nur für jeweils sehr nahkritische Temperaturen gelten dürfte, tatsächlich für die verschiedensten Stoffe auch komplizierten Molekülaufbaues sehr weit entfernt von der kritischen Temperatur anwendbar ist. Die Frage, warum das so ist , ist letzlich von der heutigen Theoretischen Physik unbeantwortet.

Die Theorie kritischer Phänomene erklärt die Eigenschaften bestimmter physikalischer Größen als eine Reihenentwicklung der reduzierten Temperatur (Tk-T)/Tk. Auch für die Dichtedifferenz ρ‘-ρ“ besteht solch eine Reihenentwicklung. Damit ist es dann möglich, eine sehr genaue Gleichung zur Bestimmung der Siededichte eines Stoffes als Temperaturfunktion abzuleiten, wenn nur einige wenige Meßwerte dazu vorliegen (s. den Artikel vom 5.7.2010 in diesem Blog “ Kritische Exponenten als mögliche Grundlage sehr genauer Stoffwertberechnungen“). Beispielrechnungen bei hoher Übereinstimmung mit Meßwerten wurden mit dem kritischen Exponenten β = 1/3 durchgeführt.

Die o.gen. Zustandsfunktion

wurde mit einer Erweiterung des für den Druck und der Dichte auf der kritischen Isotherme geltenden kritischen Phänomens des Exponenten δ = 4.4±0.4 abgeleitet. Voraussetzung dabei ist die Hypothese, daß das für die kritische Isotherme erklärte kritische Phänomen

(const- Konstante) auf Drücke weit entfernt vom kritischen Druck und auch auf Temperaturen entfernt von der kritischen Temperatur übertragen werden kann. Die mathematische Strucktur der sich mit dieser Hypothese ergebenden Gleichungen führt dann allerdings nicht zu dem Exponenten δ, sondern zu einem Exponenten RTk/pkvk für die kritische Isotherme bzw. zu RT/psv“ für eine von Tk verschiedene Temperatur.

Interessant ist, daß dieser sich aus der Rechnung ergebende Exponent der reziproke Wert des in der Technischen Thermodynamik verwendeten Realgasfaktors eines Gases im Sättigungszustand ist: ps v“/RT. Auf der kritischen Isotherme liegen Werte des reziproken Realgasfaktors für alle möglichen Stoffe oft bei 3.5 bis 4.5- also durchaus in der Größenordnung des kritischen Exponenten δ= 4.4±0.4. Wenn bedacht wird, daß der kritische Exponent um 4.4 nur auf der kritischen Isotherme in der unmittelbaren Nähe des kritischen Drucks gilt, ist der Unterschied zum reziproken Wert des Realgasfaktors evtl. durch die Erweiterung des kritischen Phänomens auf Drücke keineswegs nur in der Nähe des kritischen Drucks erklärbar. Die näherungsweise Gültigkeit der abgeleiteten o. gen. Zustandsfunktion ist durch eine Vielzahl von Nachrechnungen bei Vergleichen mit Meßwerten nachgewiesen. Sie hat den Vorteil, unabhängig von empirischen Voraussetzungen zu sein- z. B. von dem in der Technischen Thermodynamik für sogen. halbempirische Zustandsgleichungen notwendigen völlig empirischen azentrischen Faktor.

Die bisherigen Untersuchungen zur Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene auf Daten weiter entfernt von Daten des kritischen Punktes sind bisher nur auf die o.gen. kritischen Phänomene bezogen. Ergebnisse zur Kompressibilität und vor allem zur der Wärmekapazität eines Stoffes als Funktion der Temperatur liegen noch nicht vor; sie sind in Arbeit, um festzustellen, ob auch dafür Gesetzmäßigkeiten kritischer Phänomene im beschriebenen Sinne modifiziert werden können.

Posted in kritische Phänomene, Universalitätshypothese, Zustandsgleichung | Kommentare deaktiviert für Gedanken zur Universalitätshypothese kritischer Phänomene

Die Berechnung von Flüssigkeitsdaten

November 2nd, 2011

Speziell für Flüssigkeiten kann physikalisch begründet die Zustandsgleichung

abgeleitet werden. Dabei ist T die absolute Temperatur / K , p der Druck über der Flüssigkeit / MPa, ps der Dampfdruck der Flüssigkeit/ Mpa, v das molare Volumen/ cm³/mol, b das molekulare Eigenvolumen/ cm³/mol und K eine dimensionslose Konstante. Diese Gleichung gilt für Flüssigkeiten entsprechend Temperaturen niedriger Dampfdrücke bis zu Temperaturen höherer Dampfdrücke, nicht aber in der Nähe der kritischen Temperatur.

Das Moleküleigenvolumen b ist als die Summe der einzelnen Volumina, die die Moleküle des Stoffes durch ihre atomare Strucktur im Raum aufspannen, erklärt. Das Eigenvolumen erweist sich über weite Temperaturbereiche (von niedrigen bis zu hohen Temperaturen, nicht aber in der Nähe der kritischen Temperatur) als konstant. Es kann mit Stoffdaten, die für niedrige Dampfdrücke gelten, berechnet werden- z. B. mit den (p,v,T)- Daten des oft bekannten normalen Siedepunkts, ebenso ist auch die obige Größe K festgelegt. Zu den Einzelheiten der Theorie s. “ Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0).

Für etliche technisch wichtige Stoffe sind die sogen. Realgasfaktoren Z = pv/RT sowohl für die Gas- als auch für die Flüssigphase entlang einer Isotherme von niedrigen bis zu hohen Drücken erfaßt. Diese Daten sind aus Stoffdatenbanken oder aus Stoffwertsammlungen (s. z. B. W. Blanke: „Thermophysikalische Stoffgrößen“, Springer Verlag) zu entnehmen. Es handelt sich um versuchstechnisch ermittelte Werte. Die Nachrechnung dieser Werte mit den heute in physilalischer Chemie und Verfahrenstechnik bekannten Zustandsgleichungen führt oft zu Ergebnissen, die mit den Meßwerten nicht übereinstimmen. Vor allem bei Flüssigkeiten ist das so, da es für Flüssigkeiten bisher keine allgemein anwendbare und physikalisch begründete Zustandsgleichung gab. Die o.gen. Flüssigkeits- Zustandsgleichung ermöglicht es allerdings nun, Flüssigkeitsvolumina bei vorgegenem Druck und gegebener Temperatur bei weitgehender Übereinstimmung mit Meßwerten zu berechnen bzw. die Realgasfaktoren zu bestimmen.

Die Tatsache, daß die bisher auch für Flüssigkeiten angewendeten Zustandsgleichungen von van der Waals und ihre Modifikationen zu oft ungenauen Ergebnissen führen, ist als Theorie- Tatsache durchaus bekannt, da es eine physikalisch ausgearbeitete Theorie der Flüssigkeiten bisher nicht gibt. Interessant ist deshalb das Ergebnis einer Umfrage zu diesem Thema. Es wurde die Frage gestellt, ob es unterdessen Möglichkeiten zur Berechnung von Flüssigkeits- Realgasfaktoren bis zu hohen Drücken von 50 bis 100 MPa mit geringen Fehlern gegenüber Ergebnissen aus Meßwerten gibt. Es wurde gefragt: Ist es überwiegend in der Praxis noch so, daß für Flüssigkeiten nur eigens durchgeführte pvT- Messungen zum Ziel führen? Fachlich fundierte Antworten bestätigten, daß es bisher noch keine physikalisch begründeten allgemein gültigen Ergebnisse aus einer Theorie der Flüssigkeiten gibt, die es ermöglichen würde, Realgasfaktoren für Flüssigkeiten vom Dampfdruck bis zu hohen Drücken auf einer Isotherme mit ausreichender Übereinstimmung mit Meßwerten zu berechnen.

Aber es gab auch ganz andere Antworten. Z. B. die, man solle dazu unter „google scholar“ nachsehen. Oder gar keine Stellungnahmen. Oder die: Es gibt Berechnungsmöglichkeiten.

Die o. gen. speziell für Flüssigkeiten bestehende Gleichung wurde mit einer Vielzahl von Stoffbeispielen immer mit dem Ergebnis weitgehender Übereinstimmung mit Meßwerten überprüft. Einige Beispiele dazu sind im Artikel “ Erdgas- flüssig “ vom 4.3. 2010 bereits genannt. Vor allem ist auf den Artikel „Die Zustandsdaten von Flüssigkeiten- berechnet von niedrigen bis hohen Drücken“ vom 6.2.2010 in diesem Zusammenhang hinzuweisen.

Die nachfolgenden Diagramme für Realgasfaktoren solch wichtiger Stoffe wie Wasser und Kohlenstoffdioxid bei verschiedenen Temperaturen können die gute Übereinstimmung zwischen Rechnung mit obiger Gleichung und Meßwerten zeigen.

Wasser- flüssig:

Kohlenstoffdioxid CO2- flüssig:

Die gute Übereinstimmung zwischen Rechnung und den Werten aus Versuchsdaten ist für die wichtigen Beispiele Wasser und Kohlenstoffdioxid ersichtlich. Ein weitgehend linearer Verlauf des Realgasfaktors Z in Abhängigkeit vom Druck auf einer Isotherme ist ersichtlich.

Für viele Stoffe, auch technisch wichtige Stoffe, ist die Druckabhängigkeit von Flüssigkeitsdaten noch gar nicht bekannt. Nur für absolut wichtige Stoffe- wie z. B. Wasser, Kohlenstoffdioxid, Methan, Ethylen, Propan, Butan, Stickstoff, Ammoniak, Sauerstoff- sind Realgasfaktoren druckabhängig bei verschiedenen Temperaturen als allgemein zugängige Daten (ohne evtl. vorhandene Angaben aus gebührenpflichtigen Datenbanken) auf der Grundlage von Meßwerten erfaßt. Mit der o. gen. Flüssigkeitszustandsgleichung besteht nun die Möglichkeit, den Verlauf des Realgasfaktors einer Flüssigkeit zumindest als Näherung zu erfassen, wenn allein nur die pvT- Daten des normalen Siedepunkts des Stoffes vorliegen (oder auch nur das molare Volumen bei einer Temperatur niedrigen Dampfdrucks).

Die eingangs gen. Flüssigkeitszustandsgleichung wird gelöst, indem bei vorgegebenem Druck und vorgegebener Temperatur das jeweilige molare Volumen gesucht wird. Bei der überwiegenden Zahl der Lösungen liegt jeweils nur ein Volumenwert vor, so daß als Realgasfaktor immer nur ein Wert Z = pv/RT entsteht. Interessanterweise existieren aber auch p,T- Zustände von Flüssigkeiten, für die sich nach obiger Gleichung nicht nur eine Lösung für das molare Volumen ergibt, sondern sogar zwei! Das bedeutet, daß es in solchen Flüssigkeitszuständen zumindest mathematisch auch zwei Realgasfaktor- Werte gibt.

An den Beispielen Wasser und Kohlenstoffdioxid soll das näher erläutert werden.

Für Wasser bei 300 °C und einem Druck von 10 MPa ergibt sich rechnerisch ein Realgasfaktor Z1 = 0.049, der mit dem entsprechenden Wert 0.051 auf der Grundlage von Meßwerten gut übereinstimmt. Außerdem ergibt sich aber auch noch ein zweiter Wert Z2 = 0.186. Bei einem Druck von 15 MPa ebenfalls bei 300 °C ist Z1 = 0.073 und Z2 = 0.32 feststellbar. Der Wert Z1 stimmt gut mit dem auf der Basis von Meßwerten sich ergebenden Realgasfaktor 0.078 überein. Nur im Bereich der Temperatur von 300 °C und Drücken von ca. 10 bis 15 MPa ist eine zweite Lösung Z2 überhaupt feststellbar. Alle anderen untersuchten Wasser- Zustände von 100 bis 350 °C und Drücken bis 100 MPa haben immer nur eine Z- Lösung, die mit den Werten nach Messungen gut übereinstimmen.

Die Frage ist: Was bedeutet die Lösung Z2, die nur in einem eng begrenzten Druck- und Temperaturbereich erklärt ist?

Auch für Kohlenstoffdioxid sind ähnlich wie bei Wasser in einem eng begrenzten p,T- Bereich zwei Lösungen der angewendeten Flüssigkeitszustandsgleichung feststellbar, so daß für bestimmte p,T- Zustände jeweils zwei Realgasfaktoren genannt werden müssen. Für Kohlenstoffdioxid z. B. bei -40 °C und einem Druck von 2 MPa ist Z1 = 0.04 und Z2 = 0.4 feststellbar. Der Wert Z1 stimmt mit dem mit Meßwerten ermittelten Wert o.o405 gut überein. Bei einer Temperatur von 0 °C und einem Druck von 4 MPa ergibt sich Z1 = 0.0845. Dies stimmt gut dem Wert 0.08305 überein,der sich nach Meßwerten ergibt. Für einen zweiten Wert gilt Z2 = 0.172. Ähnlich wie im Fall Wasser ist die zweite Lösung in einem nur engen Zustandsbereich erklärt (ca. von -40°C bis 0 °C und relativ niedrigen Drücken).

Auch hier ist die Frage zu stellen, was bedeutet die zweite Lösung Z2, die nur in einem engem Druck- und Temperaturbereich erklärt ist?

Es gibt nur zwei Erklärungsmöglichkeiten. Prinzipiell besteht die Möglichkeit, daß die Lösung Z2 ohne eine physikalische Bedeutung allein nur durch die mathematische Strucktur der o.gen. Flüssigkeitszustandsgleichung zu Stande kommt. Sicherlich muß man diesen Fall präferieren. Die andere Möglichkeit würde folgendes bedeuten: Für einen bestimmten vorgegebenen Druck und eine bestimmte vorgegebene Temperatur einer Flüssigkeit können zwei molare Volumenwerte existieren, so daß in diesem Fall zwei Realgasfaktoren feststellbar sind. Dies würde allerdings weiter bedeuten, daß in einem engen p,T- Zustandsbereich einer Flüssigkeit zwei Modifikationen des Stoffes mit zwei unterschiedlichen Dichten existieren können – ρ1 = M/v1, ρ2 = M/v2 (M- relative Molmasse g/mol). Sollte solch eine Möglichkeit tatsächlich bestehen? Es ist sehr fraglich. Andererseits ist die evtl. Existenz der beiden Flüssigkeitsmodifikationen in einem jeweils nur sehr engen p,T- Bereich erklärt, zu dem in Bezug auf eine zweite Modifikation wegen ihrer Unwahrscheinlichkeit bisher gar keine Untersuchungen vorliegen können.

Was sollte getan werden?

Experimente z.B. mit Wasser bei ca. 300 °C und Drücken um 10 bis 15 MPa könnten darüber aufklären, ob es eine zweite Flüssigkeitsmodifikation entsprechend der obigen Flüssigkeits- Zustandsgleichung überhaupt gibt. Der Autor dieses Artikels ist dazu nicht in der Lage. Gibt es fachlich Interessierte, die die Gültigkeit und Aussagekraft der gen. Flüssigkeits- Zustandsgleichung mit den dazu notwendigen Technik- Einrichtungen überprüfen könnten und wollen? Allerdings besteht das Risiko, nur bestätigt zu bekommen, daß es nur die eine Flüssigkeitsmodifikation gibt. Falls allerdings bestätigt werden sollte, daß es in einem engen p,T- Bereich eine zweite Flüssigkeitsmodifikation geben kann, ist der wissenschaftliche Gewinn erheblich.

Posted in Dichte von Flüssigkeiten und Gasen, Theorie der Flüssigkeiten und Gase, Zustandsgleichung | Kommentare deaktiviert für Die Berechnung von Flüssigkeitsdaten

Nochmals: Stoffdaten für Nuklear- Reaktoren

Juli 22nd, 2011

Nach einer Anfrage bei Herrn Prof. Dr. Koch- Lehrstuhl Energiesysteme und Energiewirtschaft der Ruhr- Universität Bochum und einer Antwort von Herrn DI Kruse ergab sich, daß wichtige Stoffdaten für Nuklear- Reaktoren in „MATPRO- A Librery of Materials Properties for Light- Water Reactor Accident Analysis“ ( Editor: D.T. Hagmann, Idaho National Engineering Labaratory Idaho 83415) erfaßt sind. Für den Erhalt dieser u.a. Informationen ist zu danken.

Damit ist nun ein Vergleich zwischen den berechneten Dampfdrücken nach der hier begründeten physikalischen Theorie ( s. Artikel „Neue Ergebnisse zur Dampfdruckberechnung – angewendet auf flüssige Metalle und ihre Verbindungen bei der Kernschmelze“ vom 10.6.2011) und den aus der o. gen. Literaturstelle als Näherungen angegebenen Dampfdrücken möglich.

Zu betonen ist, daß in o. gen. Literaturstelle zur Ableitung der Dampfdruckfunktion die Clausius- Clapeyronsche Gleichung und nur Idealgasverhalten als Näherung bei der Bestimmung von Parametern der Berechnungsgleichung vorausgesetzt wird. Das ist bei Anwendung der im Artikel vom 10.6.2011 beschriebenen Dampfdruck- Differentialgleichung nicht der Fall.

Der mögliche Vergleich einiger Daten für Plutoniumdioxid PuO2 ist folgender:

Für flüssiges Urandioxid UO2 ergibt sich folgendes:

Es ist für PuO2 und UO2 ersichtlich: Die ungefähre nach der Größenordnung feststellbare Übereinstimmung der nach der angegebenen Dampfdruck- Differentialgleichung berechneten Dampfdrücke mit denen der MATPRO- Näherungen besteht. Zu betonen ist, daß die zur Berechnung benutzte Dampfdruckfunktion entsprechend der gen. Dampfdruck-Differentialgleichung nur einen einzigen bekannten Datenpunkt benötigt- nämlich nur den Dampfdruck bei einer bestimmten Temperatur und das dazu gehörende Flüssigkeitsvolumen. Das ist bei allen anderen Näherungen so einfach nicht der Fall. Es ist davon auszugehen, daß bei genauerer Kenntnis nur eines für den jeweiligen Stoff versuchstechnisch ermittelten Datentripels (Temperatur, Dampfdruck, Flüssigkeitsvolumen) viel genauere Dampfdruckkurven für PuO2 und UO2 angegeben werden könnten. Leider scheinen aber für Flüssigkeitsdichten und damit für die molaren Volumina zwar Einschätzungen aber keine Meßwerte vorzuliegen, so daß die Ergebnisse mit der o.gen. Dampfdruck- Differentialgleichung nur Näherungen sein können. Falls es Meßwerte für Dampfdruck und Flüssigkeitsdichte bei Temperaturen über dem Schmelzpunkt gibt, könnte damit dann sofort die Dampfdruckkurve aufgezeichnet werden. Und nicht nur das: Auch genauere Aussagen zum Verlauf der Tau- und Siededichten in Abhängigkeit von der Temperatur wären dann möglich.

Posted in Stoffdaten für Nuklearreaktoren | Kommentare deaktiviert für Nochmals: Stoffdaten für Nuklear- Reaktoren

Neue Ergebnisse zur Dampfdruckberechnung- angewendet auf flüssige Metalle und ihre Verbindungen bei der Kernschmelze

Juni 10th, 2011

1. Ableitung einer allgemein gültigen Dampfdruckfunktion

Für die Verdampfungsenthalpie Δh eines Stoffes kann aus der thermodynamischen Theorie die Gleichung

abgeleitet werden. Dabei ist T die absolute Temperatur / K, v‘ und v“ ist das molare Flüssigkeits- und das molare Sattdampfvolumen / cm³/mol dieses Stoffes. Die Funktion p(T,v) entspricht der Zustandsgleichung des jeweiligen Stoffes. Allerdings ist darauf hinzuweisen, daß die in der heutigen Technischen Thermodynamik meist angewendeten weitgehend halbempirisch genannten Zustandsgleichungen in obiger Δh- Gleichung gegenüber einer physikalisch begründeten van der Waals- Gleichung (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ – ISBN 978-3-00-027253-0) weniger genaue Ergebnisse liefern. Die angewendete Zustandsfunktion p(T,v) sollte entsprechend des Blog- Artikels vom 6.2.2010 („Die Zustandsdaten von Flüssigkeiten- berechnet von niedrigen bis hohen Drücken“) dem Gleichungssystem

bei variablen Parametern a,b entsprechen, um genauere Ergebnisse zu erreichen (R=8.314 J/mol K- allgemeine Gaskonstante, ps- Dampfdruck).

Durch die Clausius- Clapeyronsche – Gleichung

die den Zusammenhang der Steigung der Dampfdruckkurve mit der Verdampfungsenthalpie und den Tau- und Siedevolumina v“,v‘ herstellt, ist eine allgemeine Dampfdruck- Differentialgleichung

erklärt.

Diese Gleichung ist auswertbar. Die Auswertung der Differentialgleichung mit einem entsprechenden numerischen Lösungsprogramm als auch die Formulierung der analytischen Lösung ist möglich. Die Programme hierzu liegen vor.

Für Zustände niedriger bis mäßiger Drücke und den entsprechenden Temperaturen entsteht als allgemein gültige Differentialgleichung des Dampfdrucks

Dabei ist v’o das Siedevolumen der Flüssigkeit bei einer niedrigen Temperatur To, z. B. der des normalen Siedepunkts, b ist dann das Eigenvolumen des Stoffes ebenfalls bei der Temperatur To (s. o.gen. Literaturstellen).

Die Lösung dieser mathematisch nicht ganz einfachen Gleichung (Funktionswert ps ist als nichtlinearer Term in der ln- Funktion enthalten) ist möglich. Man erhält tatsächlich immer recht gut mit Meßwerten übereinstimmende Dampfdruckwerte eines Stoffes. Voraussetzung ist die Kenntnis nur eines einzigen bekannten Datenpunktes als Meßwert. Dieser bekannte Datenpunkt kann der normale Siedepunkt To mit seiner Temperatur und dem molaren Flüssigkeitsvolumen sein. Man kann also mit obiger Dampfdruckdifferentialgleichung den Dampfdruckverlauf einer Substanz für Temperaturen unterhalb und oberhalb der normalen Siedepunktstemperatur problemlos rechnerisch bestimmen.

Es ist darauf hinzuweisen, daß mit allen anderen bisher angewendeten Dampfdrucknäherungen immer mehrere (ps,T)- Meßwerte (mindestens aber 2 bekannt sein müssen), um die Dampfdruckkurve innerhalb eines Temperaturintervalls angeben zu können.

2. Der Dampfdruck hochsiedender flüssiger Metalle und ihrer Verbindungen

Flüssige Metalle und ihre Verbindungen sind meist sehr hochsiedende Substanzen. Die Messung der Eigenschaften solcher Stoffe ist schwierig- allein schon wegen der Meßtechnik bei extrem hohen Temperaturen bis zu mehreren Tausend Kelvin.

Allerdings sind für etliche flüssige Metalle und ihre Verbindungen neben den Schmelztemperaturen auch normale Siedetemperaturen bekannt. Auch Dichten sind oftmals als Meßwerte vom Schmelzpunkt bis zu Temperaturen in Richtung des normalen Siedepunkts gegeben (aus z. B. sogen. „Wire Explosions in Air“ -Experimenten), so daß in diesen Fällen sogar Aussagen zum molaren Volumen bis zum normalen Siedepunkt möglich sind.

Damit sind grundsätzlich die Anfangsbedingungen (normale Siedetemperatur und molares Volumen am normalen Siedepunkt) zur Anwendung der o. gen. Dampfdruckdifferentialgleichung gegeben. In all diesen Fällen ist es möglich, den Dampfdruckverlauf flüssiger Metalle und ihrer hochsiedenden Verbindungen als Temperaturfunktion für Zustände unterhalb und oberhalb der normalen Siedetemperatur anzugeben.

Dies soll für einige besonders interessante Fälle im Zusammenhang mit möglichen Kernschmelzen geschehen.

3. Thermophysikalische Daten für Materialien im Zusammenhang mit Kernschmelzen

Die kürzlichen Vorgänge in japanischen Kernkraftwerken, die -wie sich nun noch nachträglich herausstellt- sogar bis zu Kernschmelzen führten, rücken die Atomkraft wieder vermehrt in das öffentliche Interesse.

Die Fragen zur Beherrschbarkeit der Atomtechnologie im Havariefall sind berechtigt. Für den Fall der Kernschmelze und der damit bei ungenügender Kühlung weiter steigenden Temperatur ist es wichtig, die Eigenschaften der beteiligten Materialien genau zu kennen. Dies betrifft vor allem die Brennstäbe mit z. B. den Materialien Urandioxid, Plutoniumdioxid und Zirkonium. Es ist zu fragen, ob die thermophysikalischen Eigenschaften dieser hochschmelzenden Materialien überhaupt genügend bekannt sind. Als fundamentale Materialeigenschaften sollten zur Ermöglichung einer Voreinschätzung des Verlaufs einer möglichen Kernschmelze zumindest bekannt sein: Schmelzpunkt, normaler Siedepunkt, Dichten des Feststoffes bis zum Schmelzpunkt, Dichten der Schmelze oberhalb der Schmelztemperatur entlang der Siedelinie, Dampfdrücke bis zur normalen Siedetemperatur und darüber.

Sehr wichtig im Fall der Kernschmelze ist die Eigenschaft des sich bildenden Schmelzsees der beteiligten Materialien im System einer entstehenden Mischungslücke von U-Zr-O- Fe bzw. von Tendenzen der Verhinderung einer Entmischung durch Konvektionsströmungen in der Schmelze. Gerade aber in diesem Fall ist die Kenntnis thermophysikalischer Daten – wie z. B. des Dampfdrucks- der einzelnen Komponenten des Gemisches zur Beurteilung insgesamt der flüssigen Phase und der Gasphase als nichtideales Gemisch von ausschlaggebender Bedeutung. (Datenbanken s. GEMINI, NUCLEA, CHEMSA/ CHEMAPP, MOX)

Die Frage ist, ob das alles für die beteiligten Stoffe bekannt ist und vorliegt und genügend genau in relevanten Simulationsprogrammen für Kernschmelzen erfasst ist. Wer weiß das schon wirklich mit dem Nachweis der ausreichenden Genauigkeit oder ist die ausreichende Genauigkeit nur eine Behauptung?

Aus allgemein zugänglichen Datensammlungen (z. B. „Detherm“ der Dechema, „webelements.com“ u. a.) und speziellen mit flüssigen Metallen befassten Literaturstellen ergeben sich solche Daten leider in der vollständigen Gänze nicht und im Detail sogar widersprüchlich.

Evtl. ist es so, daß interne und nicht allgemein zugängliche Betreiber- und Firmendaten vorliegen.

Bekannt ist, daß es intensive Forschungsbemühungen gab, thermophysikalische Eigenschaften hochschmelzender Metalle durch Wire Explosions in Air- Experimente zu erfassen. Dadurch wurden Angaben zur elektrischen Leitfähigkeit und auch zur Dichte bei hohen Temperaturen gewonnen. Auch physikalisch- theoretische Untersuchungen zur kritischen Temperatur, zum kritischen Druck und zum evtl. Verlauf der Dampfdruckkurve als Extrapolation von niedrigen Meßwerten aus liegen vor (s. z.B. die Arbeiten von H. Hess, H. Schneidenbach in Z. Metallkunde).

All diese Untersuchungen und Ergebnisse belegen letztlich die für flüssige Metalle unbefriedigende Situation, thermophysikalische Daten nicht oder nur ungenau zu kennen. Auch für die Verbindungen dieser Metalle und für ihre Mischungen trifft das trotz der umfangreichen jeweils staatlichen Mittelzuflüsse für Forschungen dieser Art zu, die der Steurerzahler bezahlen mußte.

Sollte es evtl. nur eine Hoffnung sein, anzunehmen. daß AKW- Betreiberfirmen einen weiterführenden Datenbestand zu Kernreaktor- Materialien haben?

Die Anwendung der o. gen. physikalisch begründeten Dampfdruck- Differentialgleichung , deren Richtigkeit an vielen anorganischen und organischen Substanzen nachgewiesen werden kann, muß auch im Fall flüssiger Metalle und seinen Verbindungen gerechtfertigt sein. Das kann nachgewiesen werden.

Für einige flüssige Metalle liegen physikalisch und versuchstechnisch begründete Ergebnisse zum Dampfdruckverlauf und zur Dichte für Temperaturen über dem Schmelzpunkt vor. Wenn sich zeigt, daß die bisher in der Literatur als Näherungen für solche Metalle angegebenen Dampfdruckkurven mit Lösungen der o.gen. Dampfdruck- Differentialgleichung übereinstimmen, ist wohl erklärt, diese Differentialgleichung tatsächlich zur Bestimmung von Dampfdrücken flüssiger Metalle und ihren hochsiedenden Verbindungen einsetzen zu können.

Für zwei wichtige Metalle, zu denen genügend Untersuchungsergebnisse vorliegen, soll das gezeigt werden- nämlich für Uran und Eisen.

Der für Uran erwartete Dampfdruckverlauf wird in einer den bisherigen Kenntnisstand zusammenfassenden Arbeit „Vapor pressure and critical Data for Uranium“ von H. Hess, H. Schneidenbach (Z. Metallkunde 92, 2001) dargestellt. Diese Arbeit gibt die Ergebnisse verschiedener Forscher vergleichend an. Die für Uran nach Meinung der Autoren präverierende Dampfdruckkurve wird angegeben. In nachfolgendem Diagramm ist das die Kurve 1 . Die aus der o.gen. allgemeinen Differentialgleichung sich ergebenden Dampfdruckwerte für Uran sind in der Kurve 2 erfaßt.

Es ist ersichtlich: Sowohl die Ordinatenwerte als auch die Steigungen beider Kurven stimmen recht gut überein.

Auch für Eisen im flüssigen Zustand ist das etwa so feststellbar, wie das nachfolgende Diagramm zeigt.

Ergänzend ist zu sagen: Auch die Nachrechnung weiterer Beispiele flüssiger Metalle mit entsprechend bekannten Daten bestätigt die Anwendbarkeit der o. gen. Dampfdruck-Differentialgleichung. Es muß dazu jeweils nur ein Dampfdruckmeßwert und das molare Volumen bei der Meßtemperatur bekannt sein.

Es ist deshalb gerechtferigt, die o.gen. Dampfdruck-Differentialgleichung auch auf radioaktive flüssige Uran- und Plutoniumverbindungen, wie Urandioxid und Plutoniumdioxid, auf flüssiges Plutonium und Zirkonium anzuwenden.

Plutonium:

Molekülmasse: 244.0642, Schmelzpunkt: 912.5 K, Siedepunkt: 3509 K, Dichte 16.63 g/cm³ bei 914 K (s. www.webelements.com, David R. Lide: CRC Handbock of Chemistry and Physics, 90 th Edition, CRC Press, Boca Raton, Florida 2009)

Mit diesen Daten als Ausgangspunkt der Rechnung ergibt sich das nachfolgende Diagramm als Näherung für den Verlauf der Dampfdruckkurve von Plutonium bei hohen Temperaturen.

Zirkonium:

Molekülmasse: 91.224, Schmelzpunkt: 2128 K, Siedepunkt: 4682 K, Dichte (s.): 6.511 g/cm³ (s. www.webelements.com)

Die Dampfdrucknäherung von Zirkonium ist mit nachfolgendem Diagramm gegeben.

img0008_356161562

Plutoniumdioxid PuO2:

Molekülmasse 276.06, Schmelzpunkt 2673 K, Siedepunkt 3073 K, Dichte (s) 11.50 g/cm³ (s. www.webelements.com).

Das diesen Daten entsprechende Dampfdruckdiagramm ist die folgende Näherung:

Urandioxid:

Molekülmasse: 270.03, Schmelzpunkt: 2827 °C, Siedepunkt:- , Dichte (s): 10.97 g/cm³ (s. www.webelements.com, GESTIS-Stoffdatenbank des IFA)

Leider liegt zur Berechnung der Dampfdruckkurve von Urandioxid kein vollständiger p,v,T- Datensatz vor. Die Dampfdruckkurve kann so nicht angegeben werden.

Posted in flüssige Metalle, Kernschmelze | Kommentare deaktiviert für Neue Ergebnisse zur Dampfdruckberechnung- angewendet auf flüssige Metalle und ihre Verbindungen bei der Kernschmelze

Kernschmelze

März 30th, 2011

Es wird viel von Kernschmelze in Atomkraftwerken gesprochen. Der Anlaß ist die drohende oder schon stattfindende Kernschmelze in Atomkraftwerken Japans.

Nähere Überlegungen zu den Vorgängen einer Kernschmelze sind sehr angebracht.

Bei einer Kernschmelze handelt es sich letzlich um die immer größere gefährliche Aufheizung schmelzender Brennstäbe infolge ungenügender Kühlung bei sich fortsetzender nuklearer Reaktion (Eigenwärme).

Beteiligte Materialien sind oft

– Zirkonium als Umhüllung der Brennstäbe (Schmelzpunkt 1857 °C)

– Urandioxid UO2 (Schmelzpunkt 2827 ° C ) und Plutoniumdioxid PuO2 ( Schmelzpunkt 2400 ° C ) als radioaktive Metalloxide und Füllung der Brennstäbe.

Zur Schmelze kommt es also erst, nachdem die Temperatur im Reaktor bereits bedenklich äußerst hoch bis zu ca. 2000 ° C gestiegen ist.

Eine wichtige Frage ist: Kann man die Vorgänge bei einer eintretenden und sich weiter entwickelnden Kernschmelze überhaupt nachrechnen? Existieren physikalisch begründete und gangbare Berechnungsmöglichkeiten zur Einschätzung des Verlaufs einer Kernschmelze? Es handelt sich ja um Vorgänge radioaktiver flüssiger Stoffe sehr hoher Temperatur, deren Temperatur immer noch zunehmen kann.

Grundlegende Vorausetzung solcher Berechnungsmöglichkeiten ist die Kenntnis der thermophysikalischen Eigenschaften der beteiligten Stoffe nicht nur als Feststoff, sondern auch als Flüssigkeit und bei ihrer Verdampfung. Sind diese Daten ( Dampfdruck als Temperaturfunktion, Flüssigkeits- und Dampfdichte als Temperaturfunktion ) überhaupt als Meßwerte bei solch hohen Temperaturen bekannt und bis zu welchen Temperaturen?

Übliche und allgemein (ohne Gebühr ) zugängliche Stoffdatensammlungen stellen die erforderlichen Angaben für Urandioxid, Plutoniumdioxid, Zirkonium u.a. beteiligte Stoffe nicht zur Verfügung. Auch Literaturstellen zu hochschmelzenden Metallen im flüssigen Zustand bestätigen das eigentlich noch nicht ausreichende Wissen über flüssige Metalle und ihre Verbindungen (s. z.B. für Uran: H. Hess, H. Schneidenbach: Vapour Pressure and critical Data for Uranium, Z. Metallkunde 92,2001).

Es ist allerdings darauf zu verweisen, daß mit den in diesem Blog dargelegten Theorie – Ergebnissen zur Berechnung von Flüssigkeitsvolumina v‘, von Sattdampfvolumina v“ und auch von Dampfdrücken die grob näherungsweise Einschätzung dieser Stoffwerte für an Kernreaktionen und Kernschmelzen beteiligte Substanzen evtl. möglich wird. Nähere Erläuterungen dazu sind in den Artikeln dieses Blogs zu finden:

-Flüssige Metalle, 12.11.2010

-Die Berechnung von Dampfdrücken, 11.12.2009

-Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene, 7.5.2009

-Eine Zustandsgleichung für reale Gase- abgeleitet aus der Theorie kritischer Phänomene, 1.5.2009.

Die nachfolgenden Diagramme geben die Ergebnisse bisheriger Nachrechnungen der Volumina v‘,v“ für Zirkonium, Plutoniumdioxid und Plutonium, die mit den verfügbaren Daten und den o.gen. Mitteln möglich waren, an (Uran s. den Blog- Artikel vom 30.11.2010 ).

Zirkonium Zr: berechnete kritische Temperatur 6540 K.

Plutoniumdioxid PuO2,

berechnete kritische Temperatur ca.5950 K

Plutonium Pu, berechnete kritische Temperatur ca. 6935 K

Leider standen zur Nachrechnung der v‘, v“, ps- Daten nur wenige Meßwerte zur Verfügung. So war es z. B. nicht möglich für Urandioxid UO2 die notwendigen Angaben zur Berechnung dieser Daten auf einem einfachen und unentgeltlichen Weg zu beschaffen.

(Neben den gen. allgemein zugänglichen Stoffdatensammlungen wurden benutzt: www.webelements.com; http://i-systems.dechema.de/detherm; David R. Lide: CRC Handbook of Chemistry and Physics, 90 th Edition,CRC Press,Boca raton, Florida 2009; Lester R. Morss,Norman N. Edelstein,jean Fuger: The Chemistry of the Actinide and Transactinide Elements,Spinger,Dortrecht 2006)

Es ist festzustellen: Bei einer etwas verbesserten Datenlage mit v‘ und Dampfdruck- Meßwerten beim Schmelzpunkt und etwas darüber (oder evtl. sogar v‘- Meßwerten bis zum oder beim normalen Siedepunkt) läßt sich der v‘, v“, ps- Verlauf in Abhängigkeit von der Temperatur mit geringeren Fehlern mit den o. gen. Mitteln auf der Grundlage der physikalischen Theorie kritischer Phänomene einschätzen. Damit könnte man dann evtl. begründet versuchen, Modellvorstellungen des Verlaufs einer Kernschmelze zu denken.

Posted in Kernschmelze | Kommentare deaktiviert für Kernschmelze

Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur

Februar 22nd, 2011

Falls die Aufgabe besteht, die Sättigungsvolumina v‘ und v“ bzw. die Dichten ρ‘ und ρ“ eines Stoffes für Temperaturen kurz unter der kritischen Temperatur Tk dieses Stoffes rechnerisch zu bestimmen, können sich bei Verwendung bisher üblicher Zustandsgleichungen erhebliche Abweichungen gegenüber Meßwerten ergeben.

Wenn die kritischen Daten mit dem kritischen Druck und der kritischen Temperatur bekannt sind, wird selbstverständlich eine der üblichen verfahrenstechnischen Zustandsgleichungen angewendet (evtl. die van der Waals- Gleichung, die Soave- Redlich- Kwong- Gleichung, die Peng- Robinson – Gleichung oder andere). Ist auch der Dampfdruck ps bekannt, sind die Sättigungsvolumina entsprechend der jeweiligen Zustandsgleichung mit

ps = p(v‘,T), ps = p(v“,T)

berechenbar. Ganz abgesehen davon, daß sich je nach der vorausgesetzten Zustandsgleichung unterschiedliche Ergebnisse herausstellen, ist das Hauptproblem aber folgendes: Die mit herkömmlichen Zustandsgleichungen berechneten Daten für Zustände kurz unter der kritischen Temperatur stimmen oftmals gar nicht mit Meßwerten überein. Die Fehler sind groß.

Für Wasser z. B. (als einer der für die menschliche Existenz wichtigsten Stoffe) sind die sich mit der Soave- Redlich- Kwong – Gleichung berechenbaren Sättigungsvolumina für nahkritische Zustände den Meßwerten in den nachfolgenden beiden Diagrammen gegenübergestellt. Die großen Differenzen zwischen berechneten Daten und Meßwerten sind ersichtlich. Das etwa ist so nicht nur für Wasser!

Der Rechnung wurde die Soave- Redlich- Kwong- Gleichung, die eine der weltweit meist angewendeten empirischen Zustandsgleichungen ist mit

p = RT/v-b -a/v(v+b)

und

zu Grunde gelegt (dabei ist ω ein empirisch für jeden Stoff festzulegender Faktor).

Bei der Wertung der Situation ist es wichtig, nicht nur die Tatsache von teilweise großen Ungenauigkeiten herkömmlicher Zustandsgleichungen zu berücksichtigen, sondern auch vor allem die Erkenntnis, daß Zustandsgleichungen – basierend auf der klassischen van der Waals-Gleichung und ihren empirischen Weiterentwicklungen- in der unmittelbaren Nähe der kritischen Temperatur prinzipiell gar nicht mehr gültig sein können. Der Grund sind die in der Nähe des kritischen Punktes auftretenden kritischen Phänomene. Die Reichweite der zwischenmolekularen Wechselwirkungen vergrößert sich und divergiert sogar, die molekulare Individualität scheint sich zu verlieren, es gelten für unterschiedliche Stoffe sich etwa angleichende Verhaltensweisen- eben die Gesetzmäßigkeiten kritischer Phänomene. Aber das sind nicht mehr die Bedingungen und Voraussetzungen der klassischen van der Waals- Thermodynamik. Es stellt sich heraus, daß herkömmliche Zustandsgleichungen in der Umgebung des kritischen Punktes prinzipiell nicht anwendbar sind (s. z. B. hierzu F. Schwabl: „Statistische Mechanik“, Spinger- Verlag 2004).

Die aus der physikalischen Theorie kritischer Phänomene abgeleitete Beziehung

die ohne Verwendung einer herkömmlichen Zustandsgleichung besteht, gilt auch in unmittelbarer Nähe zum kritischen Punkt (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“- ISBN 978-3-00-027253-0).

Kurz unter der kritischen Temperatur gilt auch etwa

(s. z. B. Schwabl, „Statistische Mechanik“, Springer Verlag 2004). Damit kann nun sowohl das Flüssigkeitsvolumen v‘ als auch das Dampf- Sättigungsvolumen v“ als grobe Näherung für Zustände kurz unter der kritischen Temperatur berechnet werden. Es ergibt sich für das Flüssigkeitsvolumen v‘ für einige K kurz unter der kritischen Temperatur die quadratische Gleichung

die durchaus Meßwerten nahe kommende Werte für das Flüssigkeitsvolumen v‘ und für das Dampfvolumen v“ liefert.

Die oben vorausgesetzte Symmetrie der Differenz des Flüssigkeits- bzw. Dampfvolumens zum kritischen Volumen gilt i. a. jeweils nur einige K unter der kritischen Temperatur. Für von der kritischen Temperatur weiter entfernte Zustände sind bessere Lösungen erforderlich, die tatsächlich existieren. Programme zur rechnerischen Bestimmung der Sättigungsdaten für Flüssigkeits- und Dampfzustände verschiedenster Stoffe sind auf der Grundlage kritischer Phänomene abgeleitet. Die so berechneten Daten erweisen sich als den Meßwerten viel besser entsprechend als Ergebnisse mit herkömmlichen Zustandsgleichungen.

Für einige Stoffe soll das exemplarisch belegt werden.

Für Wasser sind in den beiden nachfolgenden Diagrammen die so berechneten Flüssigkeits- und Dampfvolumina für den Sättigungszustand bei verschiedenen Temperaturen angegeben.

Die für Wasser sehr deutlichen positiven Unterschiede der Berechnungsergebnisse, die mit diesen Diagrammen im Vergleich zu den eingangs angegebenen Diagrammen entsprechend der Soave- Redlich- Kwong- Gleichung festzustellen sind, sind erheblich.

Für zwei weitere Beispiele – Ethylen und Kohlenstoffdioxid- seien Ergebnisse der v‘, v“- Nachrechnung im Vergleich mit Meßwerten genannt.

Berechnete nahkritische Flüssigkeits- und Sättigungsdampfdaten für Ethylen sind in den beiden nachfolgenden Diagrammen im Vergleich mit Meßwerten dargestellt:

Die für Kohlenstoffdioxid CO2 berechneten v‘, v“- Werte sind im Vergleich mit Meßwerten und mit nach der Soave- Redlich-Kwong- Gleichung berechneten Werten in den beiden folgenden Diagrammen dargestellt:

Die erheblichen Genauigkeitsunterschiede der Rechnungen auf der Grundlage kritischer Phänomene und der aus der klassischen van der Waals- Thermodynamik entstandenen Redlich- Kwong- Gleichung vor allem im Flüssigkeitsbereich sind ersichtlich.

Für einige weitere technisch und ökologisch wichtige Stoffe seien die mit Berücksichtigung kritischer Phänomene berechenbaren v‘, v“- Werte angegeben, für die allerdings keine in allgemein zugänglichen Datensammlungen bestehenden (unentgeltlichen) Meßwerte erkennbar waren.

Die Nachrechnungen für Ozon O3 ( Tk = 261.1 K, pk = 5.53 MPa, vk = 89.3818 cm^3/mol) auf der Grundlage kritischer Phänomene für nahkritische Zustände ergeben für die Sättigungsvolumina von Flüssigkeit und Dampf die Diagramme

Auch für Schwefelwasserstoff H2 S (Tk = 373.15 K, pk = 8.937 MPa, vk = 98.5029 cm^3/mol) als Ausgangsstoff wichtiger Synthesen waren für nahkritische Zustände keine unentgeltlich zugänglichen Meßwerte verfügbar. Die auf der Grundlage kritischer Phänomene berechneten Daten sind folgende:

Daten für Stickstoffmonooxid NO kurz unter der kritischen Temperatur (Tk = 180.2 K, pk = 6.485 MPa, vk = 57.7038 cm^3/mol) sind bei Berücksichtigung kritischer Phänomene folgende:

Zu betonen ist, daß zur Ausführung der Rechnung nicht der jeweilige Dampfdruck, doch aber die Angaben zum kritischen Punkt bekannt sein müssen.

Nachdem die Sättigungsvolumina v‘, v“ für eine Temperatur nahe der kritischen Tempertur berechnet sind, kann nun das Flüssigkeits- und Gasverhalten für nahkritische Temperaturen mit z. B. der für reale Gase aus der Theorie kritischer Phänomene abgeleiteten Gleichung

nachgerechnet werden. Allerdings ist nun auch die Kenntnis des Dampfdrucks erforderlich (zur Dampfdruckberechnung s. Artikel vom 11.12.2009 „Die Berechnung von Dampfdrücken“ ).

Als ein Beispiel hierzu sei die Nachrechnung der Realgasfaktoren Z = pv/RT für Wasser bei einer Temperatur von 350 °C (Tk = 374 °C ) und 20 MPa bis zu dem hohen Druck von 100 MPa genannt. Das nachfolgende Diagramm zeigt das Ergebnis der Nachrechnung.

Die gute Übereinstimmung mit den aus Meßwerten berechneten Realgasfaktoren ist ersichtlich. Wird die Rechnung mit einer der üblichen Zustandsgleichungen ausgeführt, sind die Ergebnisse von den Meßwerten viel weiter entfernt- wie das folgende ebenfalls für Wasser bei 350 °C geltende Diagramm entsprechend der Soave- Redlich- Kwong- Gleichung zeigt.

Vor allem für Flüssigkeitszustände sind die Ergebnisse mit der Soave-Redlich-Kwong- Gleichung sehr ungünstig. Für den Gaszustand allerdings stimmen Realgasfaktor-Ergebnisse aus der herkömmlichen Soave- Redlich-Kwong- Gleichung und den sich aus der Theorie kritischer Phänomene ergebenden Werten oft gut mit Werten aus Messungen überein.

Posted in Sättigungsdaten-Flüssigkeiten und Gase | Kommentare deaktiviert für Die Berechnung von Daten für Zustände kurz unter der kritischen Temperatur

Kupfer

Januar 3rd, 2011

Schmelzpunkt: 1356 K, normaler Siedepunkt: 2868 k, molare Masse: 63.546 g/mol

Für flüssiges Kupfer liegen Dichte- Meßwerte in Abhängigkeit von der Temperatur im Bereich vom Schmelzpunkt bis 2000 K vor ( s. C. Cagran, A. Seifter, G. R. Pottlacher: Thermophysical Properties of solid and liquid copper, Schriften Forschungszentrum Jülich, Series Energy Technology, Vol.15, p 763-766, 2000). Die Dichte beim normalen Siedepunkt wurde aus diesen Daten extrapoliert. Damit ergab es sich auch für Kupfer die im Artikel „Flüssige Metalle“ vom 12.11.10 abgeleiteten Berechnungsgleichungen anzuwenden, die sich mit Gesetzmäßigkeiten kritischer Phänomene ableiten lassen (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene- ISBN 978-3-00-027253-0).

Die für flüssiges Kupfer bestehenden Volumen- Näherungen und die Einschätzung der Sattdampfvolumina für höhere Temperaturen sind in den nachfolgenden Diagrammen angegeben.

Die berechnete kritische Temperatur als grobe Näherung beträgt 5800 K. Bisherige Einschätzungen der kritischen Temperatur geben Werte zwischen 5400 bis 8000 K an(s. H. Hess : Critical Data and Vapor Pressures for Aluminium and Copper, Z. Metallkd. 1998).

Posted in Sättigungsdaten-Flüssigkeiten und Gase | Kommentare deaktiviert für Kupfer

Wolfram

Dezember 15th, 2010

Schmelzpunkt: 3680 K, normaler Siedepunkt: ca. 5800 K, molare Masse: 183.85 g/mol

Auch für das Metall Wolfram im flüssigen Zustand ist es möglich, sowohl die Flüssigkeits- als auch die Dampfvolumina entlang der Dampfdruckkurve als grobe Näherungen zu berechnen. Die s ergibt sich aus dem Artikel „Flüssige Metalle“ vom 12.10.10 und der Unterlage „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0).

Die für das Metall Wolfram als grobe Näherung berechnete kritische Temperatur bträgt 11800 K. Literaturangaben zur kritischen Temperatur entsprechen dieser Größenordnung (s. H. Hess, A. Kloss, a. Rakhel , H. Schneidenbach: Determination of Thermophysical Properties of Fluid Metals by Wire- Axplosion Experiments, International Journal of Thermophysics, Vol.20 No.4 1999).

Posted in Sättigungsdaten-Flüssigkeiten und Gase, Wolfram | Kommentare deaktiviert für Wolfram

Uran

November 30th, 2010

Schmelzpunkt: 1405 K, normaler Siedepunkt: 4200 K, molare Masse: 238.0289 g/ mol

Nachfolgend sind Diagramme für die berechneten molaren Volumina flüssigen und dampfförmigen Urans in Abhängigkeit von der Temperatur angegeben. Die dazu erforderlichen Rechnungen wurden entsprechend des Artikels „Flüssige Metalle“ vom 12.10.2010 und der Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0) ausgeführt.

Die für das Metall Uran als grobe Näherung berechnete kritische Temperatur beträgt ca. 8400 K.

Literaturstellen ebenfalls zur Einschätzung der kritischen Temperatur von Uran nennen Werte zwischen 7000 und 12000 K (s. H.Hess, H. Schneidenbach: Vopour Pressure and critical Data for Uranium, Z. Metallkunde 92,2001).

Posted in Sättigungsdaten-Flüssigkeiten und Gase, Uran | Kommentare deaktiviert für Uran